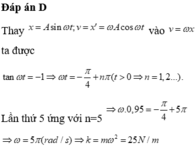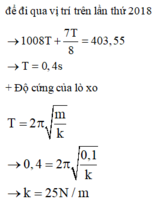Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Ta có ![]()
Khi 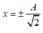 ta có
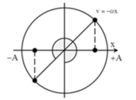
ta có ![]() khi pha dao động của vật trên đường tròn đơn vị là π/4 hoặc 3π/4 rad. (Mỗi chu kì có 2 lần vận tốc của vật v = -ωx).
khi pha dao động của vật trên đường tròn đơn vị là π/4 hoặc 3π/4 rad. (Mỗi chu kì có 2 lần vận tốc của vật v = -ωx).
Tại t = 0 vật qua VTCB theo chiều dương → pha ban đầu là –π/2 rad.
Ta có 7 = 3.2 + 1 → t = 0,825 = 3T + 3T/8 = 27T/8
→ T = 0,24 s → k = 69 N/m.

Đáp án D
Tại thời điểm t = 0,95 s, vận tốc của vật:
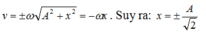
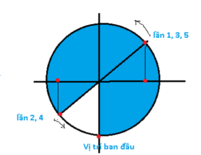
Trong một chu kì vật đi qua vị trí có v = - ω x hai lần. Lần thứ 5 vật đi qua vị trí thỏa mãn hệ thức đó là
![]()
Độ cứng của lò xo: k = 25 N/m

ko chắc đâu nha
Áp dụng công thức đẳng lập với thời gian:
\(x^2+\dfrac{v^2}{\omega^2}=A^2\) thay \(v=-\omega x\) được \(2x^2=A^2\Rightarrow x=\pm\dfrac{A\sqrt{2}}{2}\)
với \(\omega\) là hằng số dương \(v=-\omega x\) nên v và x trái dấu
khi \(x=\dfrac{A\sqrt{2}}{2}\Leftrightarrow v< 0\) hay vật đi theo chiều âm
khi \(x=-\dfrac{A\sqrt{2}}{2}\Leftrightarrow x>0\) hay vật đi theo chiều dương
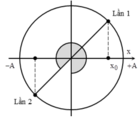
Lần thứ nhất vật qua vị trí có \(v=-\omega x\) là tại \(x=\dfrac{A\sqrt{2}}{2}\)Thời gian vật đi đến đây kể từ t=0 (ở VTCB theo chiều dương) là: \(\dfrac{T}{4}+\dfrac{T}{8}=\dfrac{3T}{8}\)
Lần thứ 5 vật cũng qua vị trí có\(v=-\omega x\) là tại \(x=\dfrac{A\sqrt{2}}{2}\)
Thời gian vật đi đến đây kể từ t=0 (ở VTCB theo chiều dương) là: \(\dfrac{3t}{8}+2t=\dfrac{19t}{8}=402,95s\Rightarrow t\approx169,7\)
\(t=2\pi\sqrt{\dfrac{m}{k}}=169,7\Rightarrow k=\dfrac{4\pi^2m}{t^2}=...\)
bn tự vẽ hình minh họa nha

Khoảng thời gian giữa 2 lần liên tiếp động ăng bằng thế năng là T/4
\(\Rightarrow \dfrac{T}{4}=\dfrac{\pi}{40}\)
\(\Rightarrow T = \dfrac{\pi}{10}\)
\(\Rightarrow \omega=\dfrac{2\pi}{T}=20(rad/s)\)
Biên độ dao động: \(A=\dfrac{v_{max}}{\omega}=\dfrac{100}{20}=5(cm)\)
Ban đầu, vật qua VTCB theo chiều dương trục toạ độ \(\Rightarrow \varphi=-\dfrac{\pi}{2}\)
Vậy PT dao động là: \(x=5\cos(20.t-\dfrac{\pi}{2})(cm)\)