Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương pháp: Sử dụng công thức tính lực căng dây của con lắc đơn dao động điều hòa
Cách giải:
+ Biên độ dao động của con lắc: α 0 = 6 0 = π / 30 rad
+ Khi con lắc ở vị trí có
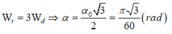
=> Lực căng dây của con lắc:
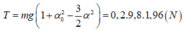
=> Chọn D

Lực căng dây cực tiểu tại vị trí biên:
\(T_{min}=mg(3.\cos\alpha_0-2\cos\alpha_0)=mg.\cos\alpha_0\)
\(\Rightarrow 0,2.10.\cos\alpha_0=1\)
\(\Rightarrow \alpha_0=60^0\)
Tại vị trí thế năng bằng động năng thì cơ năng là: \(W=W_t+W_đ=2W_t\)
\(\Rightarrow mgl(1-\cos\alpha_0)=2.mgl(1-\cos\alpha)\)
\(\Rightarrow \cos\alpha=\dfrac{1+\cos\alpha_0}{2}=\dfrac{3}{4}\)
\(\Rightarrow \alpha=41,4^0\)
Lực căng dây: \(T=mg(3\cos\alpha-2\cos\alpha_0)=0,2.10.(3.\dfrac{3}{4}-2.\dfrac{1}{2})=2,5(N)\)
Lực căng dây: \(T=mg(3\cos \alpha-2\cos \alpha_0)\)
Lực căng dây cực đại ở VTCB: \(T_{max}=mg(3-2\cos \alpha_0)=1\)
\(\Rightarrow 0,2.10.(3-2\cos \alpha_0)=1\)
\(\Rightarrow \cos\alpha_0=\dfrac{5}{4}\), vô lý
Bạn xem lại đề nhé.

Với con lắc đơn, ta có hệ số hồi phục \(k=\frac{mg}{l}\)
Lực hồi phục: \(F_{hp}=-kx\)
Với x là li độ dài, \(x=\alpha l\)
Suy ra: \(F_{hp}=-\frac{mg}{l}.\alpha l=-mg\alpha\) \(\Rightarrow F_{hpmax}=mg\alpha_0\) \(\Rightarrow\alpha_0=\frac{F_{hpmax}}{mg}=\frac{0,1}{0,1.10}=0,1rad\)(1)
Lực căng dây: \(\tau=mg\left(3\cos\alpha-2\cos\alpha_0\right)=mg\left(3\left(1-2\sin^2\frac{\alpha}{2}\right)-2\left(1-2\sin^2\frac{\alpha_0}{2}\right)\right)=mg\left(1+\alpha_0^2-\frac{3}{2}\alpha^2\right)\)(do góc \(\alpha\) rất nhỏ nên ta lấy gần đúng)
Tại vị trí \(W_t=\frac{1}{2}W_đ\Leftrightarrow W=3W_t\Leftrightarrow\alpha_0^2=3\alpha^2\Leftrightarrow\alpha=\frac{\alpha_0}{\sqrt{3}}\)
Như vậy, lực căng dây tại vị trí này là: \(\tau=mg\left(1+\alpha_0^2-\frac{3}{2}\alpha^2\right)=mg\left(1+\alpha_0^2-\frac{3}{2}\frac{\alpha_0^2}{3}\right)=mg\left(1+\frac{\alpha_0^2}{2}\right)\)
Thay từ (1) vào ta đc: \(\tau=0,1.10\left(1+\frac{0,1^2}{2}\right)=1,005N\)

Chọn D

Thế năng: Et = mghB = mgl(1 - cosa)
Năng lượng: E =Et max= mghmax= mgll.(1 - cosa0)
(Năng lượng bằng thế năng cực đại ở biên)
- Động năng:
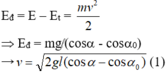
Xét tại vị trí B, hợp lực tác dụng lên quả nặng là lực hướng tâm: ![]() (ở đây ký hiệu T là lực căng)
(ở đây ký hiệu T là lực căng)
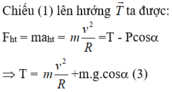
Thế R = l và (1) vào (3) ta được T = mg(3cosa - 2cosa0)
Khi Eđ = 2Et → Et = E/3 ↔ mgl(1 - cosa) = mgl.(1 - cosa0)/3→cosα = (2 + cosα0)/3
→ T = mg(2 – cosa0).

Đáp án B
Lực căng của dây treo có giá trị cực đại gấp 4 lần giá trị cực tiểu nên
![]()
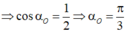
Chọn mốc thế năng tại vị trí cân bằng, bỏ qua lực cản W d = W 2 .
Tại thời điểm động năng bằng thế năng thì
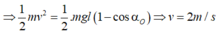

- Lực căng của dây treo có giá trị cực đại gấp 4 lần giá trị cực tiểu nên:
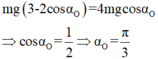
- Chọn mốc thế năng tại vị trí cân bằng, bỏ qua lực cản. Tại thời điểm động năng bằng thế năng thì: 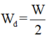
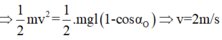
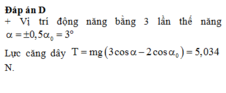
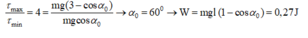

Cơ năng tại vị trí ban đầu :
\(W=mgl\left(1-cos\alpha_o\right)=\dfrac{1}{2}l\left(J\right)\)
Cơ năng tại vị trí : \(W_đ=3W_t\)
\(W=W_t+3W_t=4W_t\) \(=4mgl\left(1-cos\alpha\right)=\dfrac{1}{2}l\)
\(\Leftrightarrow4mg\left(1-cos\alpha\right)=\dfrac{1}{2}\)
\(\Leftrightarrow cos\alpha=\dfrac{7}{8}\)
\(T=mg\left(3cos\alpha-2cos\alpha_o\right)\)
\(=\dfrac{13}{8}\left(N\right)\)