Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Li độ dài ban đầu của nó là:
$x=\alpha.l=2$cm
Có: $\omega^2=\frac{g}{l}$
Áp dụng công thức liên hệ giữa li độ và vận tốc trong dao động điều hoà ta có:
$A^2=x^2+\frac{v^2}{\omega^2}$
$\Rightarrow A=2\sqrt2$cm

Hệ số hồi phục: \(k=\frac{mg}{l}\)
Lực kéo về: \(F=k.x=\frac{mg}{l}.\alpha.l=mg.\alpha\)
Góc lệch: \(\alpha=\frac{\alpha_0}{2}=\frac{0,1}{2}=0,05rad\)
\(\Rightarrow F=0,1.10.0,05=0,05N\)
Độ lớn của lực kéo về:\(F = ks\), \(s\) là li độ cong của con lắc đơn.
Vật ở vị trí có li độ cong bằng lửa biên độ tức
\(F = k \frac{S_0}{2}= \frac{k.\alpha_0.l}{2}\) (do \(s_0 = \alpha_0 .l\))
\(=m\omega ^2.\frac{\alpha_0.l}{2}=\frac{mg\alpha_0}{2}=\frac{0,1.10.0,1}{2}=5.10^{-2}N.\)
Vậy lức kéo về tại vị trí đó là \(F = 5.10^{-2}N.\)

Khi vật qua VTCB thì vận tốc đạt cực đại
\(\Rightarrow v_{max}=\omega.A=\sqrt{\dfrac{g}{l}}.\alpha_0.l=\sqrt{g.l}\alpha_0\)
\(\Rightarrow l=\dfrac{v_{max}^2}{g.\alpha_0^2}=25000(cm)=250m\)

1/ Bước sóng: \(\lambda=v/f=0,2m\)
Ta có: \(2.[\dfrac{AB}{\lambda}+0,5]=2.[\dfrac{1,1}{0,2}+0,5]=12\)
Do \(\dfrac{1,1}{0,2}+0,5=6\) là giá trị nguyên, mà ở 2 đầu A, B không có cực đại cực tiểu, nên số điểm không dao động trên đoạn AB là: \(12-2=10\)
Chọn C.
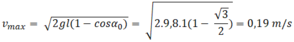
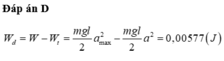
Cơ năng của vật:
\(W=mgl(1-\cos\alpha_0)=m.9,8.0,5.(1-\cos30^0)=2,45(2-\sqrt 3).m\)
Khi \(W_đ=2W_t\) thì cơ năng:
\(W=W_đ+W_t=W_đ+0,5W_đ=1,5W_đ\)
\(\Rightarrow W = 1,5.0,5mv^2=0,75mv^2\)
\(\Rightarrow 2,45(2-\sqrt 3).m=0,75mv^2\)
\(\Rightarrow v = \sqrt{\dfrac{2,45.(2-\sqrt 3)}{0,75}}=0,94\) (m/s)
thây giỏi ghê !