Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

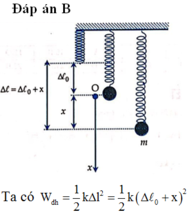
Đáp án B
Chọn Oxy như hình vẽ:
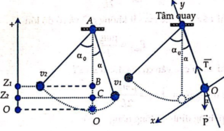
+ Chọn mốc tính thế năng tại vị trí thấp nhất của vật
Cơ năng của vật ở vị trí 1 ứng với góc ![]() là
là
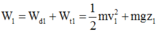
![]()
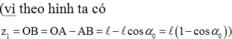
Cơ năng của vật ở vị trí 1 ứng với góc ![]() là
là
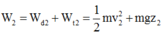
![]()
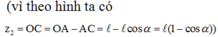
Bỏ qua sức cản không khí, thì cơ năng của vật là một đại lượng bảo toàn tức là W1 = W2
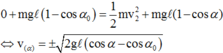
Gia tốc theo thành phần Oy là gia tốc hưóng tâm
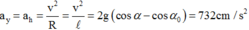
Theo định luật II Niu tơn ta có: 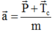 chiếu lên Ox ta được:
chiếu lên Ox ta được:
![]()
Vậy gia tốc của vật nặng của con lắc khi ![]() = 30° có độ lớn bằng:
= 30° có độ lớn bằng:
![]()

Từ đồ thị ta thấy
Vật nặng cao nhất lò xo biến dạng ![]() thế năng đàn hồi có giá trị tương ứng với 1 đơn vị chia trên trục tọa độ.
thế năng đàn hồi có giá trị tương ứng với 1 đơn vị chia trên trục tọa độ.
Vật nặng thấp nhất lò xo biến dạng ![]() thế năng đàn hồi có giá trị tương ứng với 9 đơn vị chia trên trục tọa độ
thế năng đàn hồi có giá trị tương ứng với 9 đơn vị chia trên trục tọa độ

![]()
Mặt khác 4 đơn vị chia ứng với 80 mJ. Vậy 1 đơn vị chia ứng với 20mJ ta được:

Mặt khác xét ở vị trí cân bằng: Ở vị trí cân bằng lực đàn hồi cân bằng với trọng lực nên:
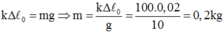

Kéo quả nặng đến vị trí lò xo giãn 5 cm → A = 5 cm.
Tần số góc ω = Căn (k/m) = Căn (25/0.25) = 10 rad/s.
Tại thời điểm t = 0 vật đi qua vị trí cân bằng lần đầu tiên → φ = -π/2 rad.
→ phương trình dao động của quả nặng là x = 5cos(10t – π/2) cm.

Đáp án C
Ta giải nhanh khi đã nắm được công thức:
![]()
Ở bài toán này: thế năng của lò xo bằng 3 lần động năng, tức là n = 3. Do vậy
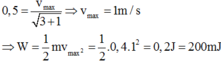

Quãng đường đi được trong t=2s
\(x=10+5\cdot2+2\cdot2^2=28\left(m\right)\)
Vận tốc của vật ở thời điểm t = 2s là
\(V=\dfrac{x}{t}=\dfrac{28}{2}=14\)(m/s)

Đáp án B
Ta giải nhanh khi đã nắm được công thức:
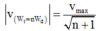
Ở bài toán này: Động năng bằng 1/9 lần cơ năng theo định luật bảo toàn ta có:
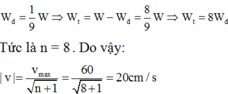


chỗ tính s của bạn bấm máy lại ha, ra 9,999 làm tròn thành 10 nhé
còn kêu người khác xem lại bài họ thì cũng phải chỉ ra lỗi sai trong bài người khác ha.
Từ phương trình li độ dài: \(s=10cos\left(2t\right)\)
Tại \(t=\dfrac{\pi}{12}s\), ta có: \(s=10cos\left(2t\right)=10cos\left(2.\dfrac{\pi}{12}\right)=5\sqrt{3}cm\)
Thế năng tại thời điểm đó:
\(W_t=\dfrac{1}{2}m\omega^2s^2=\dfrac{1}{2}0,2.2^2.\left(5\sqrt{3}.10^{-2}\right)^2=3.10^{-3}J\)
Cơ năng của con lắc đơn:
\(W=\dfrac{1}{2}m\omega^2S_0^2=\dfrac{1}{2}.0,2.2^2.\left(10.10^{-2}\right)^2=4.10^{-3}J\)
⇒ Động năng của con lắc tại thời điểm đó:
\(W_đ=W-W_t=4.10^{-3}-3.10^{-3}=10^{-3}J\)