Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đổi 15p = \(\frac{1}{4}\)h
Gọi vận tốc ca nô khi dòng nước yên lặng là x (km/h) ĐK: x > 0
Vận tốc của ca nô khi xuôi dòng: x + 4 (km/h)
Vận tốc của ca nô khi ngược dòng: x - 4 (km/h)
Thời gian ca nô xuôi dòng : \(\frac{80}{x+4}\)(h)
Thời gian ca nô ngược dòng : \(\frac{72}{x-4}\)(h)
Ta có PT: \(\frac{72}{x-4}-\frac{80}{x+4}=\frac{1}{4}\)
\(\Leftrightarrow\frac{288\left(x+4\right)-320\left(x-4\right)}{\left(x+4\right)\left(x-4\right)}=\frac{x^2-16}{\left(x+4\right)\left(x-4\right)}\)
\(\Leftrightarrow x^2+32x-2448=0\)
Giai PT ta được x1 = 36 (Nhận)
x2 = -68 (Loại)
Vậy vận tốc thực của ca nô là 36km/h

Gọi vận tốc riêng của cano là \(x\left(km/h\right),x>4\).
Vận tốc khi cano đi xuôi dòng là: \(x+4\left(km/h\right)\).
Thời gian cano đi xuôi dòng là: \(\frac{120}{x+4}\left(h\right)\).
Vận tốc khi cano đi ngược dòng là: \(x-4\left(km/h\right)\).
Thời gian cano đi ngược dòng là: \(\frac{96}{x-4}\left(h\right)\).
Ta có phương trình:
\(\frac{96}{x-4}-\frac{120}{x+4}=1\)
\(\Rightarrow96\left(x+4\right)-120\left(x-4\right)=\left(x-4\right)\left(x+4\right)\)
\(\Leftrightarrow x^2+24x-880=0\)
\(\Leftrightarrow x=20\)(vì \(x>4\))
.

Gọi vận tốc thực của ca nô là x (x > 0, km/h)
Đổi 15 phút = 15 60 = 1 4 h
*) Xuôi dòng:
Vận tốc của ca nô là x + 4 (km/h) → Thời gian xuôi dòng của ca nô là 80/(x+4) (h)
*) Ngược dòng
Vận tốc ngược dòng của ca nô là x – 4 (km/h) → Thời gian ngược dòng của ca nô là 72/(x-4) (h)
Vì thời gian xuôi dòng ít hơn thời gian ngược dòng là 15 phút nên ta có phương trình:
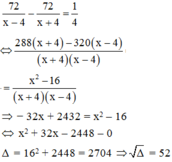
Phương trình có hai nghiệm
x = −16 + 52 = 36 (tmdk)
x = −16 – 52 = −68 (loại)
Vậy vận tốc thực của ca nô là 36 km/h
Đáp án: A

gọi vận tốc thực là x(x>4)km/h
vận tốc khi xuôi dòng là x+4 km/h
vận tốc khi ngược dòng là x-4 km/h
thời gian ca nô đi xuôi dòng là \(\dfrac{80}{x+4} \)h
thời gian ca nô đi ngược dòng là \(\dfrac{80}{x-4} \)h
vì tổng thời gian ca nô đi xuôi dòng và ngược dòng là 8h20p=\(\dfrac{25}{3} \)h
nên ta có pt \(\dfrac{80}{x+4} \)+\(\dfrac{80}{x-4} \)=\(\dfrac{25}{3} \)
giải pt x=-0.8 Ktm điều kiện
x= 20 TM
vậy vận tốc thực của ca nô là 20km/h

Gọi vận tốc thực của ca nô là x ( km/h ; x > 4 )
Vận tốc khi ca nô xuôi dòng = x + 4 (km/h)
Vận tốc khi ca nô ngược dòng = x - 4 (km/h)
Thời gian ca nô xuôi dòng = 136/x+4 (giờ)
Thời gian ca nô ngược dòng = 91/x-4 (giờ)
Tổng thời gian xuôi dòng và ngược dòng là 7h30' = 15/2h
=> Ta có phương trình : \(\frac{136}{x+4}+\frac{91}{x-4}=\frac{15}{2}\)
<=> \(\frac{136\left(x-4\right)}{\left(x-4\right)\left(x+4\right)}+\frac{91\left(x+4\right)}{\left(x-4\right)\left(x+4\right)}=\frac{15}{2}\)
=> 15( x2 - 16 ) = 2( 227x - 180 )
<=> 15x2 - 454x + 120 = 0
Δ' = b'2 - ac = (-227)2 - 15.120 = 49 729
Δ' > 0, áp dụng công thức nghiệm thu được x1 = 30 (tm) ; x2 = 4/15 (ktm)
Vậy vận tốc thực của ca nô là 30km/h

Gọi vận tốc riêng của ca nô là x ( km/h , x > 3 )
Vận tốc ca nô khi xuôi dòng = x + 3
Vận tốc ca nô khi ngược dòng = x - 3
=> Thời gian ca nô đi khi xuôi dòng = 40/x+3
Thời gian ca nô đi khi ngược dòng = 40/x-3
Thời gian xuôi dòng ít hơn thời gian ngược dòng 20 phút = 1/3 giờ
=> Ta có phương trình : \(\frac{40}{x-3}-\frac{40}{x+3}=\frac{1}{3}\)
<=> \(\frac{3\cdot40\left(x+3\right)}{3\left(x-3\right)\left(x+3\right)}-\frac{3\cdot40\left(x-3\right)}{3\left(x-3\right)\left(x+3\right)}=\frac{\left(x-3\right)\left(x+3\right)}{3\left(x-3\right)\left(x+3\right)}\)
<=> \(120x+360-120x+360=\left(x-3\right)\left(x+3\right)\)
<=> \(720=\left(x-3\right)\left(x+3\right)\)
<=> \(720=x^2-9\)
<=> \(x^2=729\)
<=> \(x=\pm\sqrt{729}=\pm27\)
Vì x > 0 => x = 27
Vậy vận tốc riêng của ca nô = 27km/h

Gọi \(a,b\) lần lượt là vận tốc riêng của ca nô và vận tốc dòng nước \(\left(a>b>0\right)\).
Thời gian ca nô đi xuôi dòng khúc sông \(60km\) là : \(\dfrac{60}{a+b}\left(h\right)\).
Thời gian ca nô đi ngược dòng \(48km\) là : \(\dfrac{48}{a-b}\left(h\right)\).
Theo đề bài thì \(\dfrac{60}{a+b}+\dfrac{48}{a-b}=6\left(1\right)\).
Thời gian ca nô đi xuôi dòng \(40km\) là : \(\dfrac{40}{a+b}\left(h\right)\).
Thời gian ca nô đi ngược dòng \(80km\) là : \(\dfrac{80}{a-b}\left(h\right)\)
Cũng theo đề bài, ta có : \(\dfrac{40}{a+b}+\dfrac{80}{a-b}=7\left(2\right)\).
Từ \((1)\) và \((2)\), ta có hệ phương trình :
\(\left\{{}\begin{matrix}\dfrac{60}{a+b}+\dfrac{48}{a-b}=6\\\dfrac{40}{a+b}+\dfrac{80}{a-b}=7\end{matrix}\right.\left(I\right)\)
Đặt : \(x=\dfrac{20}{a+b}\) và \(y=\dfrac{16}{a-b}\). Hệ \((I)\) được viết lại thành :
\(\left\{{}\begin{matrix}3x+3y=6\\2x+5y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=2\\2x+5y=7\end{matrix}\right.\)
Hay : \(\left\{{}\begin{matrix}5x+5y=10\\2x+5y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=3\\x+y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{20}{a+b}=1\\\dfrac{16}{a-b}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=20\\a-b=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a=36\\a+b=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=18\\b=2\end{matrix}\right.\) (thỏa mãn).
Vậy : Vận tốc riêng của ca nô là \(18(km/h)\) và vận tốc dòng nước là \(2(km/h).\)
Gọi vận tốc riêng của cano là x (km/h) với x>0
Gọi vận tốc của dòng nước là y (km/h) với y>0 và y<x
Vận tốc cano khi xuôi dòng: \(x+y\) (km/h)
Vận tốc cano khi ngược dòng: \(x-y\) (km/h)
Do cano xuôi dòng 60km và ngược dòng 48km hết 6h nên ta có:
\(\dfrac{60}{x+y}+\dfrac{48}{x-y}=6\)
Do cano xuôi dòng 40km và ngược dòng 80km thì hết 7h nên ta có:
\(\dfrac{40}{x+y}+\dfrac{80}{x-y}=7\)
Ta được hệ: \(\left\{{}\begin{matrix}\dfrac{60}{x+y}+\dfrac{48}{x-y}=6\\\dfrac{40}{x+y}+\dfrac{80}{x-y}=7\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{120}{x+y}+\dfrac{96}{x-y}=12\\\dfrac{120}{x+y}+\dfrac{240}{x-y}=21\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{120}{x+y}+\dfrac{96}{x-y}=12\\\dfrac{144}{x-y}=9\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x-y=16\\\dfrac{120}{x+y}+\dfrac{96}{16}=12\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x-y=16\\x+y=20\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=18\\y=2\end{matrix}\right.\)
Gọi vận tốc riêng của canoo là x ( x>0
vận tốc cano đi xuôi là x + 4 (km/h)
thời gian cano đi xuôi là : \(\frac{80}{x+4}\)km/ h
vận tốc cano đi ngc là ; x - 4 (km/h)
thời gian cano đi ngc hết là \(\frac{72}{x-4}\)
ta lại có thời gian khi đi xuôi ít hơn thời gian đi ngc là 15 ph= \(\frac{1}{4}\)h
\(\Rightarrow\)pt \(\frac{80}{x+4}\)+\(\frac{1}{4}\)=\(\frac{72}{x-4}\)
giải ra ta đc x = 36