Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(a,b\) lần lượt là vận tốc riêng của ca nô và vận tốc dòng nước \(\left(a>b>0\right)\).
Thời gian ca nô đi xuôi dòng khúc sông \(60km\) là : \(\dfrac{60}{a+b}\left(h\right)\).
Thời gian ca nô đi ngược dòng \(48km\) là : \(\dfrac{48}{a-b}\left(h\right)\).
Theo đề bài thì \(\dfrac{60}{a+b}+\dfrac{48}{a-b}=6\left(1\right)\).
Thời gian ca nô đi xuôi dòng \(40km\) là : \(\dfrac{40}{a+b}\left(h\right)\).
Thời gian ca nô đi ngược dòng \(80km\) là : \(\dfrac{80}{a-b}\left(h\right)\)
Cũng theo đề bài, ta có : \(\dfrac{40}{a+b}+\dfrac{80}{a-b}=7\left(2\right)\).
Từ \((1)\) và \((2)\), ta có hệ phương trình :
\(\left\{{}\begin{matrix}\dfrac{60}{a+b}+\dfrac{48}{a-b}=6\\\dfrac{40}{a+b}+\dfrac{80}{a-b}=7\end{matrix}\right.\left(I\right)\)
Đặt : \(x=\dfrac{20}{a+b}\) và \(y=\dfrac{16}{a-b}\). Hệ \((I)\) được viết lại thành :
\(\left\{{}\begin{matrix}3x+3y=6\\2x+5y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=2\\2x+5y=7\end{matrix}\right.\)
Hay : \(\left\{{}\begin{matrix}5x+5y=10\\2x+5y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=3\\x+y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{20}{a+b}=1\\\dfrac{16}{a-b}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=20\\a-b=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a=36\\a+b=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=18\\b=2\end{matrix}\right.\) (thỏa mãn).
Vậy : Vận tốc riêng của ca nô là \(18(km/h)\) và vận tốc dòng nước là \(2(km/h).\)
Gọi vận tốc riêng của cano là x (km/h) với x>0
Gọi vận tốc của dòng nước là y (km/h) với y>0 và y<x
Vận tốc cano khi xuôi dòng: \(x+y\) (km/h)
Vận tốc cano khi ngược dòng: \(x-y\) (km/h)
Do cano xuôi dòng 60km và ngược dòng 48km hết 6h nên ta có:
\(\dfrac{60}{x+y}+\dfrac{48}{x-y}=6\)
Do cano xuôi dòng 40km và ngược dòng 80km thì hết 7h nên ta có:
\(\dfrac{40}{x+y}+\dfrac{80}{x-y}=7\)
Ta được hệ: \(\left\{{}\begin{matrix}\dfrac{60}{x+y}+\dfrac{48}{x-y}=6\\\dfrac{40}{x+y}+\dfrac{80}{x-y}=7\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{120}{x+y}+\dfrac{96}{x-y}=12\\\dfrac{120}{x+y}+\dfrac{240}{x-y}=21\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{120}{x+y}+\dfrac{96}{x-y}=12\\\dfrac{144}{x-y}=9\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x-y=16\\\dfrac{120}{x+y}+\dfrac{96}{16}=12\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x-y=16\\x+y=20\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=18\\y=2\end{matrix}\right.\)

Gọi vận tốc cano là x (km/h), vận tốc dòng nước là y (km/h)
Khi cano xuôi dòng:
12/(x+y) + 12/(x-y) = 2,5 (1)
Khi cano xuôi dòng 4km và ngược dòng 8km:
4/(x+y) + 8/(x-y) = 4/3 (2)
Từ (1) và (2) => 1/(x+y) = 1/12 và 1/(x-y) = 1/8
=> x+y =12 và x-y =8
=> x = (12+8)/2 =10
y =x-8 =2
Vận vận tốc cano là 10 km/h, vận tốc dòng nước là 2 km/h
HOK TOT

Gọi vận tốc cano là x (km/h), vận tốc dòng nước là y (km/h)
Khi cano xuôi dòng:
12/(x+y) + 12/(x-y) = 2,5 (1)
Khi cano xuôi dòng 4km và ngược dòng 8km:
4/(x+y) + 8/(x-y) = 4/3 (2)
Từ (1) và (2) => 1/(x+y) = 1/12 và 1/(x-y) = 1/8
=> x+y =12 và x-y =8
=> x = (12+8)/2 =10
y =x-8 =2
Vận vận tốc cano là 10 km/h, vận tốc dòng nước là 2 km/h.
@học tốt nha!
Gọi vận tốc cano là x (km/h), vận tốc dòng nước là y (km/h)
Khi cano xuôi dòng:
12/(x+y) + 12/(x-y) = 2,5 (1)
Khi cano xuôi dòng 4km và ngược dòng 8km:
4/(x+y) + 8/(x-y) = 4/3 (2)
Từ (1) và (2) => 1/(x+y) = 1/12 và 1/(x-y) = 1/8
=> x+y =12 và x-y =8
=> x = (12+8)/2 =10
y =x-8 =2
Vận vận tốc cano là 10 km/h, vận tốc dòng nước là 2 km/h.

Gọi vận tốc cano là x (km/h,x>0) và vận tốc dòng nước là y(km/h,y>0)
Vận tốc cano xuôi dòng là x+y(km/h)
Vận tốc cano ngược dòng là x-y(km/h)
thời gian cano xuôi dòng khúc sông 60km là \(\frac{60}{x+y}\)
Thời gian cano ngược dòng 48km là \(\frac{48}{x-y}\)
tổng thời gian là 6h nên ta có pt: \(\frac{60}{x+y}\)+\(\frac{48}{x-y}\)=6
Tưiong tự ta có pt \(\frac{40}{x+y}\)+\(\frac{80}{x-y}\)=7
Ta có hpt \(\hept{\begin{cases}\frac{60}{x+y}+\frac{48}{x-y}=6\\\frac{40}{x+y}+\frac{80}{x-y}=7\end{cases}}\)
Đặt ẩn phụ giải ra ta đc \(\hept{\begin{cases}x+y=20\\x-y=16\end{cases}}\)
nên x=18,y=2
kl

gọi vận tốc thực là x(x>4)km/h
vận tốc khi xuôi dòng là x+4 km/h
vận tốc khi ngược dòng là x-4 km/h
thời gian ca nô đi xuôi dòng là \(\dfrac{80}{x+4} \)h
thời gian ca nô đi ngược dòng là \(\dfrac{80}{x-4} \)h
vì tổng thời gian ca nô đi xuôi dòng và ngược dòng là 8h20p=\(\dfrac{25}{3} \)h
nên ta có pt \(\dfrac{80}{x+4} \)+\(\dfrac{80}{x-4} \)=\(\dfrac{25}{3} \)
giải pt x=-0.8 Ktm điều kiện
x= 20 TM
vậy vận tốc thực của ca nô là 20km/h

Đáp án A
Đổi 7 giờ 30 phút= 15/2 (h)
Gọi vận tốc thực của ca nô là x (km/h; x > 3).
vận tốc của ca nô khi xuôi dòng sông từ A đến B là: x + 3 (km/h)
Vận tốc của ca nô khi ngược dòng sông từ B về A là: x – 3 (km/h)
Thời gian của ca nô khi xuôi dòng sông từ A đến B là: 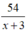 (h)
(h)
Thời gian của ca nô khi ngược dòng sông từ B về A là: 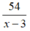 (h)
(h)
Do ca nô chạy xuôi dòng sông từ A đến B rồi chạy ngược dòng từ B về A hết tất cả 7 giờ 30 phút nên ta có phương trình:
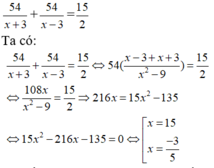
Ta thấy chỉ có x = 15 thỏa mãn điều kiện x > 3.
Vậy vận tốc thực của ca nô là 15 (km/h).

Đổi 8 giờ 6 phút = 81/10 (h)
Gọi vận tốc thực của ca nô là x (km/h), x > 2
Vận tốc của ca nô khi xuôi dòng sông từ A đến B là x + 2 (km/h)
Vận tốc của ca nô khi ngược dòng sông từ B về A là x – 2 (km/h)
Thời gian của ca nô khi xuôi dòng sông từ A đến B là 72/(x+2) (h)
Thời gian của ca nô khi ngược dòng song từ B về A là 72/(x-2) (h)
Do ca nô chạy xuôi dòng từ A đến B rồi chạy ngược dòng từ B về A hết tất cả 8 giờ 6 phút nên ta có phương trình:
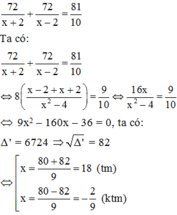
Vậy vận tốc thực của ca nô là 18 (km/h)
Đáp án: A

Gọi vận tốc ca nô là x
Gọi vận tốc dòng nước là y (đơn vị km/h ; x,y > 0 )
Theo đề ta có
vận tốc khi xuôi dòng : x + y
vận tốc khi ngược dòng : x - y
2h30p=2.5h=5/2h
1h20p=4/3h
\(\frac{S}{v_{xuôi}}+\frac{S}{v_{ngược}}=\frac{12}{x+y}+\frac{12}{x-y}=\frac{5}{2}\)
\(\frac{4}{x+y}+\frac{8}{x-y}=\frac{4}{3}\)
Từ trên ta có HPT \(\hept{\begin{cases}\frac{12}{x+y}+\frac{12}{x-y}=\frac{5}{2}\\\frac{4}{x+y}+\frac{8}{x-y}=\frac{4}{3}\end{cases}}\)
Gọi \(x+y=a;x-y=b\)
\(\Leftrightarrow\hept{\begin{cases}\frac{12}{a}+\frac{12}{b}=\frac{5}{2}\\\frac{4}{a}+\frac{8}{b}=\frac{4}{3}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\frac{12}{a}+\frac{12}{b}=\frac{5}{2}\\\frac{12}{a}+\frac{24}{b}=\frac{12}{3}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\frac{12}{b}=\frac{3}{2}\\\frac{12}{a}+\frac{24}{b}=\frac{12}{3}\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}b=8\\\frac{12}{a}+\frac{24}{8}=\frac{12}{3}\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}b=8\\a=12\end{cases}}\)
\(\Rightarrow b=x-y=8;a=x+y=12\)
\(\Rightarrow x=10;y=2\)
PT Trên có 1 nghiệm (x;y) = (10;2 )