Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tính áp suất p' của khí trong bình .
Lúc đầu khí trong bình (1) có \(\begin{cases}V_1\\p=10^5Pa\\T=300K\end{cases}\) bình (2) có: \(\begin{cases}V_2=2V_1\\p\\T\end{cases}\)
Số mol khí trong hai bình \(n=\frac{3pV_1}{RT}\)
Lúc sau, khí trong bình (1) có \(\begin{cases}V_1\\p'\\T_1=273K\end{cases}\) bình (2) có \(\begin{cases}V_2=2V_1\\p'\\T_2=330K\end{cases}\)
Số mol khí trong bình (1): \(n_1=\frac{p'V_1}{RT_1}\), trong bình (2): \(n_2=\frac{2p'V_1}{RT_2}\)
\(n=n_1+n_2\Leftrightarrow\frac{3pV_1}{RT}=\frac{p'V_1}{RT_1}+\frac{2p'V_2}{RT_2}\)
\(\frac{3p}{T}=p'\left(\frac{1}{T_1}+\frac{2}{T_2}\right)\) suy ra \(p'=1,024.10^5Pa\)

Đáp án: C
Ban đầu, khí Nito có khối lượng mm, thể tích V, áp suất p, nhiệt độ T
PT: p 1 V = m M R T 1
- Sau một thời gian, khí Heli có khối lượng m′, thể tích V, áp suất p2, nhiệt độ T
PT: p 2 V = m ' M R T 2
Lấy 2 1 ta được:
p 2 p 1 = m ' m ↔ 0,8 1 = m ' m → m ' = 0,8 m
=> Lượng khí Nito đã thoát ra:
Δ m = m − m ' = m − 0,8 m = 0,2 m = 0,2.1.28 = 5,6 g
Số mol khí Nito thoát ra ngoài là: n = m M = 5,6 28 = 0,2 m o l
Vậy lượng khí đã thoát ra ngoài bằng: 0,2mol

Trạng thái 1: \(\left\{{}\begin{matrix}p_1=10^5Pa\\T_1=27^oC=300K\end{matrix}\right.\)
Trạng thái 2: \(\left\{{}\begin{matrix}p_2=5\cdot10^5Pa\\T_2=???\end{matrix}\right.\)
Quá trình đẳng tích:
\(\dfrac{p_1}{T_1}=\dfrac{p_2}{T_2}\Rightarrow\dfrac{10^5}{300}=\dfrac{5\cdot10^5}{T_2}\)
\(\Rightarrow T_2=1500K=1227^oC\)

Ta có : T1 = toC + 273 = 30 + 273 = 303oK
p1 = 2 bar = 2 . 105 Pa
p2 = 4 bar = 4 . 105
Vì quá trình là đẳng tích , áp dụng định luật Charles ta có
\(\frac{p_1}{p_2}=\frac{T_1}{T_2}\)→ T2 = \(\frac{p_2.T_1}{p_1}=\frac{4.10^5.303}{2.10^5}\)= 606oK
Vậy để áp suất tăng lên gấp đôi , ta phải tăng nhiệt độ lên 606oK
* Trạng thái 1: T1 = 273 + 30 = 303 K
p1 = 2 bar
* Trạng thái 2: T2 = ? p2 = 2p1
* Vì thể tích bình không đổi nên:
\(\frac{P1}{T1}=\frac{P2}{T2}\Rightarrow T2=\frac{P2.T1}{P1}=\frac{2P1.T1}{P1}\) = 2T1 = 606 K
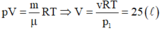
\(P.V=nRT\Rightarrow V=\frac{nRT}{P}=\frac{1.R.\left(27+273\right)}{10}\approx249\left(m^3\right)\)