
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) Vì ∠xOt và ∠tOy là 2 góc kề bù nên
∠xOt + ∠tOy = 180°
=> ∠xOt = 180° - ∠tOy
∠xOt = 180° - 60°
∠xOt = 120°
Vậy ∠xOt = 120°
3,Om là tia phân giác của yot
=>mOt=\(30^0\)
On là tia phân giác của xOt
=>nOt=\(60^0\)
Om là tia phân giác của yOt
On là tia phân giác của xOt
=>Ot nằm giữa Om,On
nOt+mOt=nOm
nOm=30+60=90
=>......................

2006 . 125 + \(\dfrac{1000}{126}\) . 2005 - 888 = 265774,6984



Đặt A = \(\dfrac{1}{3}+\dfrac{1}{15}+\dfrac{1}{35}+\dfrac{1}{63}+\dfrac{1}{99}+\dfrac{1}{143}+\dfrac{1}{195}\)
\(=\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+\dfrac{1}{7.9}+\dfrac{1}{9.11}+\dfrac{1}{11.13}+\dfrac{1}{13.15}\)
\(\Rightarrow2A=\)\(=\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+\dfrac{2}{7.9}+\dfrac{2}{9.11}+\dfrac{2}{11.13}+\dfrac{2}{13.15}\)
\(\Rightarrow2A=\) \(\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{13}-\dfrac{1}{15}\)
\(\Rightarrow2A=\) \(\dfrac{1}{1}-\dfrac{1}{15}=\dfrac{14}{15}\)
\(\Rightarrow A=\dfrac{14}{15}:2=\dfrac{7}{15}\)
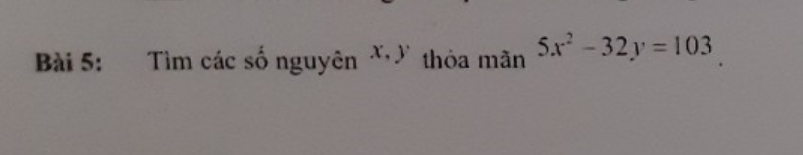


 giúp mik với ạ mik cần gấp! Cảm ơn trước 🥰
giúp mik với ạ mik cần gấp! Cảm ơn trước 🥰


Do 103 là số nguyên tố lẻ và 32y chẵn nên \(5x^2\) lẻ
Do đó \(x^2\) lẻ
\(\Leftrightarrow x^2:4\) dư 1
Mà \(32y⋮4\Leftrightarrow5x^2-32y:4\) dư 1
Mà \(103:4\) dư 3 nên PT vô nghiệm
Mik cảm ơn