Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C M D E
dễ thấy tứ giác ADME là hình chữ nhật do có 3 góc vuông
nên chu vi ADME=2(AE+EM)
mà do ABC vuông cân nên góc ECM =45 độ nên MEC vuông cân tại E nên EM=EC
nên chu vi ADME=2(AE+EM)=2(AE+EC)=2AC là không đổi
b.DE=AM nhỏ nhaasrt khi M là hình chiếu của A lên BC

a, \(MD//AB,AB\perp AC\left(gt\right)\Rightarrow MD\perp AC\Rightarrow\widehat{MDA}=90^0\)
\(ME//AC,AB\perp AC\left(gt\right)\Rightarrow ME\perp AB\Rightarrow\widehat{MEA}=90^0\)
Tứ giác MDAE có 3 góc vuông nên là hình chữ nhật.
b, Hình chữ nhật có 1 đường chéo là đường phân giác thì là hình vuông
Do đó: \(MDAE\) là hình vuông \(\Leftrightarrow\) AM là tia phân giác của \(\widehat{DAE}\)
Vậy M là giao điểm giữa tia p/g của \(\widehat{DAE}\) và cạnh BC thì MDAE là hình vuông.
c, MDAE là hình chữ nhật (cmt) \(\Rightarrow DE=AM\) (tính chất của HCN)
AM ngắn nhất khi AM là đường cao.
Vậy DE ngắn nhất khi AM là đường cao của \(\Delta ABC.\)
Chúc bạn học tốt.

a) -Xét tứ giác AHMK có:
\(\widehat{AHM}=\widehat{HAK}=\widehat{AKM}=90^0\) nên AHMK là hình chữ nhật.
=>\(AM=HK\) (t/c hình chữ nhật).
b) Gỉa sử \(AM\perp HK\).
- Xét hình chữ nhật AHMK có:
\(AM\perp HK\) (gt)
=>AHMK là hình vuông.
=>AM là tia phân giác của \(\widehat{BAC}\) (t/c hình vuông).
- Vậy điểm M là giao điểm của đường phân giác \(\widehat{BAC}\) với cạnh BC thì
\(AM\perp HK\).
c) - Kẻ \(AM'\perp BC\) tại M'
=>\(AM\ge AM'\) (quan hệ giữa đường vuông góc và đường xiên).
- minAM=AM' ⇔\(AM\perp BC\) tại M.
Mà \(AM=HK\) =>- minHK=AM' ⇔\(AM\perp BC\) tại M.
- Vậy điểm M là chân đường vuông góc kẻ từ A đến BC thì K có độ dài nhỏ nhất.

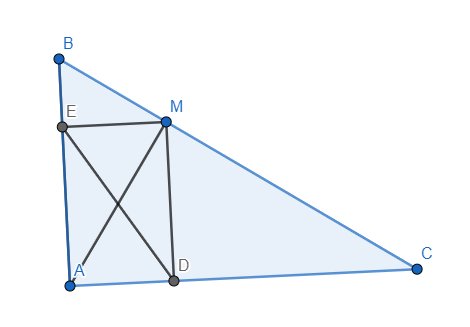
Do MD//AB và \(AB\perp AD\) nên \(MD\perp AD\) hay \(\widehat{ADM}=90^o\). Hoàn toàn tương tự, ta có \(\widehat{AEM}=90^o\). Mà \(\widehat{DAE}=90^o\) nên tứ giác ADME là hình chữ nhật. Do đó \(DE=AM\). Như vậy, ta quy về tìm vị trí của M trên BC để AM nhỏ nhất. Kẻ đường cao AH của tam giác ABC thì H cố định. Ta thấy AH và AM lần lượt là đường vuông góc và đường xiên kẻ từ A lên BC nên \(AM\ge AH\). Dấu "=" chỉ xảy ra khi \(M\equiv H\) hay M là chân đường vuông góc hạ từ A lên BC.
