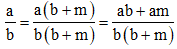Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\left(1-\dfrac{1}{3}\right)\left(1-\dfrac{1}{6}\right)\left(1-\dfrac{1}{10}\right)...\left(1-\dfrac{1}{780}\right)\)
\(=\dfrac{2}{3}.\dfrac{5}{6}.\dfrac{9}{10}.....\dfrac{779}{780}\)\(=\)

a) A=\(\dfrac{2003.2004-1}{2003.2004}=\dfrac{2003.2004}{2003.2004}-\dfrac{1}{2004}=1-\dfrac{1}{2003.2004}\)
B = \(\dfrac{2004.2005-1}{2004.2005}=\dfrac{2004.2005}{2004.2005}-\dfrac{1}{2004.2005}=1-\dfrac{1}{2004.2005}\)
Vì \(\dfrac{1}{2003.2004}>\dfrac{1}{2004.2005}\)
\(\Rightarrow1-\dfrac{1}{2003.2004}< 1-\dfrac{1}{2004.2005}\)
Vậy A < B
b) \(\left(3X-2^4\right).7^5=2.7^6.\dfrac{1}{2009^0}\)
\(\left(3X-2^4\right).7^5=2.7^6.1\)
\(\left(3X-2^4\right).7^5=2.7^6\)
\(\left(3X-2^4\right).=2.7^6:7^5\)
\(3X-2^4=2.7\)
\(3X-16=14\)
\(3X=16+14=30\)
\(X=30:3=10\)
Vậy X = 10
1/ \(A=\dfrac{2003.2004-1}{2003.2004}=\dfrac{2003.2004}{2003.2004}-\dfrac{1}{2003.2004}=1-\dfrac{1}{2003.2004}\)
\(B=\dfrac{2004.2005-1}{2004.2005}=\dfrac{2004.2005}{2004.2005}-\dfrac{1}{2004.2005}=1-\dfrac{1}{2004.2005}\)
Vì \(1-\dfrac{1}{2003.2004}< 1-\dfrac{1}{2004.2005}\Leftrightarrow A< B\)
2/ \(\left(3x-2^4\right).7^5=2.7^6.\dfrac{1}{2009^0}\)
\(\Leftrightarrow\left(3x-2^4\right).7^5=2.7^6.1\)
\(\Leftrightarrow3x-2^4=2.7^6:7^5\)
\(\Leftrightarrow3x-2^4=2.7\)
\(\Leftrightarrow3x-16=14\)
\(\Leftrightarrow3x=30\)
\(\Leftrightarrow x=10\left(tm\right)\)
Vậy ..

Ta có :
\(\dfrac{a}{b}=\dfrac{a.\left(b+d\right)}{b.\left(b+d\right)}=\dfrac{ab+bd}{b^2+bd}\)
\(\dfrac{a+c}{b+d}=\dfrac{b\left(a+c\right)}{b\left(b+d\right)}=\dfrac{ab+bc}{b^2+bd}\)
Ta so sánh :
\(\dfrac{ab+bd}{b^2+bd}\) và \(\dfrac{ab+bc}{b^2+bd}\)
Vì cùng mẫu nên ta chỉ so sánh :
\(ab+bd\) và \(ab+bc\)
\(\Rightarrow\) Ta tiếp tục so sánh :
\(bd\) và bc thì ta có : bd < bc (1)
Từ 1, suy ra :
\(\dfrac{a}{b}< \dfrac{a+c}{b+c}\)
Mà \(\dfrac{a}{b}< \dfrac{c}{d}\)
Suy ra : \(\dfrac{a}{b}< \dfrac{a+c}{b+d}< \dfrac{c}{d}\) (đpcm)

tính chất trên gọi là tính chất bắc cầu, ta so sánh hai phân số với một số (phân số) thứ 3.