Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số hạt dẻ trên mỗi ô (bắt đầu từ ô thứ nhất) theo thứ tự đó lập thành cấp số cộng ( u n ) có u 1 = 7 , d = 5.
Gọi n là số ô trên bàn cờ thì u 1 + u 2 + ⋯ + u n = 25450 = S n .
Ta có 25450 = S n = n u 1 + n n − 1 2 d = 7 n + n 2 − n 2 .5
⇔ 5 n 2 + 9 n − 50900 = 0 ⇔ n = 100
Chọn đáp án B

Chọn D.
Số hạt dẻ trên mỗi ô (bắt đầu từ ô thứ nhất) theo thứ tự đó lập thành cấp số cộng có u1 = 7; d = 5 .
Gọi n là số ô trên bàn cờ thì u1 + u2 + L + un = 25450 = Sn
Ta có 25450 = Sn = ![]() 5n2 + 9n – 50900 = 0
5n2 + 9n – 50900 = 0
Hay n = 100.

-
Để chứng minh sau hữu hạn bước sẽ không thực hiện chuyển bi được nữa, ta quan sát rằng mỗi bước chuyển bi, tổng số bi trong các ô liên tiếp tăng lên 1 đơn vị. Ban đầu có 2023 viên bi, và sau mỗi bước chuyển bi, tổng số bi trong các ô liên tiếp tăng lên 1 đơn vị. Vì số lượng ô là vô hạn, nên sau một số bước chuyển bi, tổng số bi trong các ô liên tiếp sẽ vượt quá 2023. Do đó, sau hữu hạn bước sẽ không thực hiện chuyển bi được nữa.
-
Để chứng minh P, Q, D, H đồng viên, ta sử dụng tính chất của tam giác nội tiếp và ngoại tiếp.
Vì tam giác ABC nội tiếp (O), ngoại tiếp (I), nên ta có:
- Giao điểm của EF và BC là D.
- Giao điểm của AG và EF là H.
- Giao điểm của AG và (I) là M.
Ta cần chứng minh P, Q, D, H đồng viên, tức là chúng nằm trên một đường thẳng.
Áp dụng định lí Pascal cho đường tròn ngoại tiếp (O) và đường tròn nội tiếp (I), ta có:
- Điểm P = AB ∩ EF.
- Điểm Q = AC ∩ EF.
- Điểm D = BC ∩ PQ.
Vì P, Q, D nằm trên cùng một đường thẳng PQ, nên ta chỉ cần chứng minh H nằm trên đường thẳng PQ.
Áp dụng định lí Pascal cho đường tròn ngoại tiếp (O) và đường tròn nội tiếp (I), ta có:
- Điểm H = AG ∩ EF.
- Điểm M = BC ∩ OI.
- Điểm D = PQ ∩ OI.
Vì H, M, D nằm trên cùng một đường thẳng OI, nên H nằm trên đường thẳng PQ.
Vậy ta đã chứng minh được rằng P, Q, D, H đồng viên.

a) Diện tích hình vuông ban đầu bằng 1.1 = 1 (đvdt)
Vì người ta nối các trung điểm của cạnh hình vuông để tạo ra hình vuông mới nên diện tích hình mới sẽ bằng một nửa hình trước.
Do đó ta có \({u_1} = {S_1} = 1,q = \frac{1}{2}\)
Vậy \({S_n} = 1.\frac{{1 - {{\left( {\frac{1}{2}} \right)}^n}}}{{1 - \frac{1}{2}}} = {\left( {\frac{1}{2}} \right)^{n - 1}}\)
b) \(S = \frac{1}{{1 - \frac{1}{2}}} = 2\)

Chọn D.
Gọi u1; u2; u3 tạo thành cấp số cộng.
Theo đề bài: u1 + 2; u2 + 3; u3 + 9 là ba số liên tiếp tạo thành cấp số nhân.
Theo đề bài: 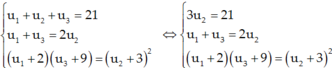
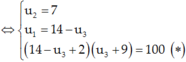
Giải (*): (16 – u3)(u3 + 9) = 100 ⇔ -u32 + 7u3 + 44 = 0 ⇔ u3 =11 ∨ u3 = - 4
Với u3 = 11 ⇒ u1 = 3.
Với u3 = -4 ⇒ u1 = 18.

Gọi 3 số đã cho là \(u_1;u_2;u_3\), theo thứ tự là 3 số của một cấp số cộng
Còn cấp số nhân \(\left(v_n\right)\). Theo giả thiết ta có hệ :
\(\Leftrightarrow\begin{cases}v_1+v_2+v_3+v_4=93\left(a\right)\\v_1=u\left(1\right)_1\\u_1+d=v_1q\left(2\right)\\u_1+2d=v_1q^2\left(3\right)\end{cases}\)
\(\Leftrightarrow\begin{cases}v_1\left(1+q+q^2\right)=93\left(a\right)\\d=u_1\left(q-1\right)\left(1V2\right)\left(4\right)\\6d=u_3-u_1=u_1\left(q^2-1\right)\left(2V3\right)\left(5\right)\end{cases}\)
\(\Leftrightarrow\begin{cases}u_1\left(1+q+q^2\right)=93\left(a\right)\\u_1\left(q-1\right)=\frac{1}{6}u_1\left(q^2-1\right)\left(4V5\right)\left(6\right)\\d=u_1\left(q-1\right)\end{cases}\)
Từ (1) và (2) cho ta phương trình (4). Còn từ (2) và (3) cho phương trình (5). Mặt khác ừ (4) và (5) cho phương trình (6)
Do \(u_1\ne0,q\ne1\Rightarrow\left(6\right)\Leftrightarrow1=\frac{1}{6}\left(q+1\right)\Leftrightarrow q=5\)
Theo (a) : \(v_1+5v_1+25v_1=93\Leftrightarrow u_1=3\)
Vậy 3 số cần tìm là : 3,15,75

Đáp án D
Gọi ô chứa hạt thóc thỏa mãn đề bài là ô thứ n ( n ∈ N , n > 1 ) . Khi đó

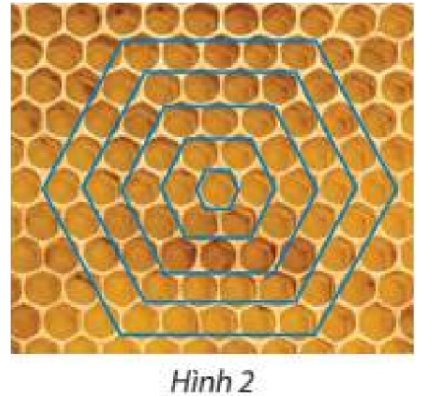

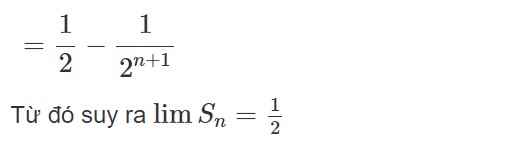

Dãy số chỉ số ô trên vòng là: \(u_1=6;u_2=12;u_3=18;...\)
Ta thấy: \(u_{n+1}=u_n+6\)
Vậy ô trên các vòng theo thứ tự tạo thành cấp số cộng có công sai d = 6.