Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có giản đồ véc tơ:
U U U R MB phi
Ta có \(\sin\varphi=\frac{U_{MB}}{U}\)
nên: \(\sin\varphi_1=\frac{U_{MB1}}{U}\)(*)
\(\sin\varphi_2=\frac{U_{MB2}}{U}\)
Mà \(U_{MB2}=2\sqrt{2}U_{MB1}\) nên: \(\sin\varphi_2=2\sqrt{2}\sin\varphi_1\)
Mặt khác: Do \(\left|\varphi_1\right|+\left|\varphi_2\right|=90^0\) nên \(\sin\varphi_2=\cos\varphi_1\), lại có: \(\sin^2+\cos^2=1\)
Giải ra ta đc: \(\sin\varphi_1=\frac{1}{3}\)
Thay vào (*) ta đc: \(U_{MB}=\frac{U}{3}=50V\)
\(\cos\varphi_2=\sin\varphi_1=\frac{1}{3}\)

Đáp án C
+ Hai giá trị của L để cho cùng một điện áp hiệu dụng trên cuộn cảm thỏa mãn: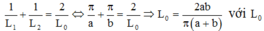
là giá trị của cảm kháng để điện áp hiệu dụng trên cuộn cảm cực đại.
+ Thay đổi L để U R C trễ pha 0,5 π so với U => đây là giá trị L để điện áp hiệu trên cuộn cảm cực đại
=> L = Lo

Ta có Z L − Z C = 10 Ω.
→ Khi tăng biến trở R từ giá trị R = 20 Ω thì công suất tiệu thụ luôn giảm.
Đáp án D

Ta có R 1 v à R 2 là hai nghiệm của phương trình R 2 − U 2 P R + Z L − Z C 2 = 0 ⇔ R 2 – 250 R + 14400 = 0
→ R 1 = 160 Ω v à R 2 = 90 Ω .
Đáp án C
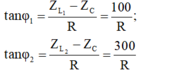
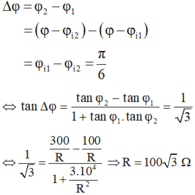
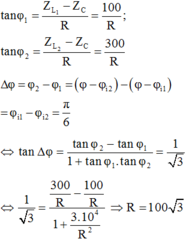
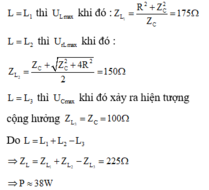

f=50 .chép thiếu ,hi