Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tổng số học sinh giỏi là: 45 – 13 = 32
Số học sinh chỉ giỏi Văn là: 32 – 25 = 7
Số học sinh chỉ giỏi Toán là: 32 – 17 =15
Số học sinh giỏi cả hai môn là: 32 – 7 – 15 = 10.

Sơ đồ học sinh lớp 10A: 25 bạn 20 bạn 15 bạn 5 1 6 7
Số học sinh thích môn toán và tiếng anh và văn là:(25+15+20)-(5+7+1+6)=42(bạn)
Số học sinh không thích môn nào là:45-42=3(học sinh)
eh8 ihgggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggg

Đáp án A
Theo giả thiết đề bài cho, ta có biểu đồ Ven:
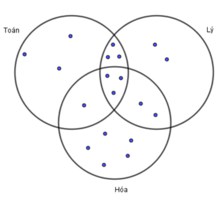
Dựa vào biểu đồ Ven ta thấy:
Số học sinh chỉ giỏi Toán và Lý (không giỏi Hóa) là: 6−3=3 (em)
Số học sinh chỉ giỏi Toán và Hóa (không giỏi Lý) là: 4−3=1 (em)
Số học sinh chỉ giỏi Lý và Hóa (không giỏi Toán) là: 5−3=2 (em)
Số học sinh chỉ giỏi một môn Toán là: 10−3−3−1=3 (em)
Số học sinh chỉ giỏi một môn Lý là: 10−3−3−2=2 (em)
Số học sinh chỉ giỏi một môn Hóa là: 11−1−3−2=5 (em)
Số học sinh giỏi ít nhất một trong ba môn là:
3+2+5+1+2+3+3=19 (em)

Số học sinh chỉ giỏi Toán là:
20-10=10(bạn)
Số học sinh chỉ giỏi Lý là:
20-10=10(bạn)
Số học sinh chỉ giỏi Hóa là:
45-10-10=25(bạn)

Đáp án C
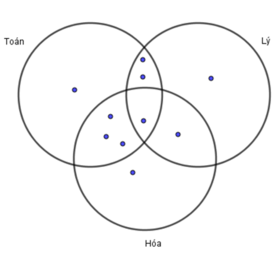
Số học sinh giỏi toán, lý mà không giỏi hóa: 3−1=2.
Số học sinh giỏi toán, hóa mà không giỏi lý: 4−1=3.
Số học sinh giỏi hóa, lý mà không giỏi toán: 2−1=1.
Số học sinh chỉ giỏi môn lý: 5−2−1−1=1.
Số học sinh chỉ giỏi môn hóa: 6−3−1−1=1.
Số học sinh chỉ giỏi môn toán: 7−3−2−1=1.
Số học sinh giỏi ít nhất một (môn toán, lý, hóa) là số học sinh giỏi 1 môn hoặc 2 môn hoặc cả 3 môn: 1+1+1+1+2+3+1=10.
bn ơi bn cho mik hỏi cái câu hỏi số hs......toán lý hóa cái câu ng ta hỏi đấy là như nào ạ mik đọc mik k hiểu lắm
 giúp em với ạ
giúp em với ạ
Gọi A là tập hợp các học sinh của lớp 10A;
V là tập hợp các học sinh giỏi môn Văn và T là tập hợp các học sinh giỏi môn Toán của lớp 10A.
Kí hiệu |X| là số phần tử của tập hợp hữu hạn X.
Ta có
Đáp án D