Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Có tất cả \(\frac{6.5}{2}=15\) (đường thẳng)
b) Cái này thì đơn giản, bạn tự làm

a) Số đường thằng nhiều nhất có được khi 6 điểm phân biệt không có 3 điểm nào thẳng hàng. Khi đó nối 2 điểm bất kỳ tạo được 1 đường thẳng, số đưởng thảng là: 6 x 5 : 2 = 15 đường thẳng.
Kể tên 15 đường thẳng; AB, AC, AD, AE, AF, BC, BD, BE, BF, CD, CE, CF, DE, DF, EF
b) Khi 6 điểm cùng nằm trên 1 đường thẳng thì số đưởng thẳng tạo thành chỉ có 1 đường thẳng.

có: 5.(5-1):2=10(đường thẳng)
đó là đường thẳng: AB;AC;AD;AE;BC;BD;BE;CD;CE;DE

A sẽ nối với 6 điểm còn lại, các điểm còn lại cũng nối với điểm kia
Tổng số đường thẳng (nếu tính thế) là: 6 x 7 = 42 (đường thẳng)
Nếu thế, mổi đường thẳng đã tính 2 lần
Số đường thẳng thực là: 42 : 2 = 21 (đường thẳng)
Đáp số: 21 đường thẳng
Chúng là: AB, AC, AD, AE, AG, AH, BC, BD, BE, BG, BH, CD, CE, CG, CH, DE, DG, DH, EG, EH, GH

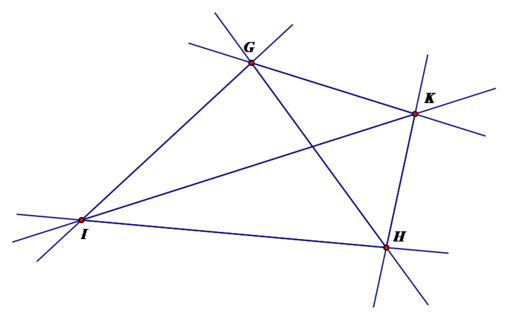
- Qua điểm G và mỗi điểm I, H, K ta vẽ được 3 đường thẳng là: GI, GH, GK.
- Qua điểm H và mỗi điểm I, K ta vẽ được 2 đường thẳng là: HI, HK (nếu tính cả điểm G sẽ bị trùng vì ở trên đã có đường thẳng GH rồi).
- Qua điểm I và điểm K ta vẽ được 1 đường thẳng là IK (không tính các điểm còn lại vì sẽ bị trùng, tương tự với điểm K)
Như vậy, qua bốn điểm I, H, K, G ta vẽ được tất cả 6 đường thẳng, đó là các đường thẳng: GI, GH, GK, HI, HK, IK.
3 đường thẳng phân biệt là BA;CA;DA
6 đoạn thẳng là BA;CA;DA;BC;CD;BD