Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
+ Tia đỏ vừa vặn phản xạ toàn phần, thì ta có thể lập luận để thấy rằng toàn bộ các tia khác cũng bị phản xạ toàn phần trên AC và khi đến BC đều ló hết ra ngoài

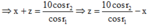
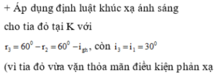
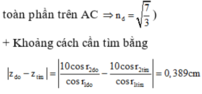

Chọn đáp án C.
n sin A = sin i ⇒ n d sin A = sin i d ⇒ 1 , 532 sin 30 0 = sin i d ⇒ i d ≈ 50 0 n t sin A = sin i t ⇒ 1 , 5867 sin 30 0 = sin i t ⇒ i t ≈ 52 , 5 0
⇒ δ = i t − i d = 2 , 5 0 .

Chọn đáp án C.
δ = ( n t − n d ) A = ( 1 , 68 − 1 , 62 ) 6 0 = 0 , 36 0 ⇔ 0 , 006 ( r a d ) .

Uh, theo suy luận của bạn mình thấy cũng có lý :)
Tuy nhiên, bài toán này mình thấy nó khá mập mờ, chẳng có phương án nào hợp lý cả.
Bài này đúng là cần dùng phương pháp loại trừ, tuy nhiên ở đây mình loại trừ D, vì nếu tia ló // với AC thì sẽ chẳng có tia nào ló ra cả vì thằng đỏ trung với cạnh AC thì các tia màu khác sẽ bị phản xạ toàn phần.
Đáp án C là hợp lý.

Phương pháp: Áp dụng công thức tính góc lệch giữa tia tới và tia ló khi lăng kính có góc chiết quang nhỏ
Cách giải: Áp dụng công thức tính góc lệch ta có:
D = (n-1)A = (1,55-1). 6 0 = 3 , 3 0
Đáp án C

Chọn đáp án A
Áp dụng công thức lăng kính: S i n i 1 = n . sin r 1 S i n i 2 = n . sin r 2 r 1 + r 2 = A D = ( i 1 + i 2 ) − A
+ Đối với tia đỏ: s i n i 1 = n d . sin r 1 d ⇒ sin r 1 d = sin 60 0 n d ⇒ r 1 d = 34 , 22 0 r 1 d + r 2 d = A ⇒ r 2 d = A − r 1 d = 15 , 78 0 s i n i 2 d = n . sin r 2 d ⇒ sin r 2 d = n d sin r 2 d ⇒ i 2 d = 24 , 76 0 D = ( i 1 + i 2 d ) − A = 60 0 + 24 , 76 0 − 50 0 = 34 , 76 0
+ Đối với tia tím: s i n 60 0 = n t . sin r 1 t ⇒ r 1 t = 33 , 24 0 r 1 t + r 2 t = A ⇒ r 2 t = A − r 1 t = 16 , 76 0 s i n i 2 t = n . sin r 2 t ⇒ sin r 2 t = n t sin r 2 t ⇒ i 2 t = 27 , 1 0 D = i 1 + i 2 d − A = 60 0 + 27 , 1 0 − 50 0 = 37 , 1 0
+ Góc hợp bởi giữa hai tia đỏ và tia tím sau khi ló ra khỏi lăng kính: D t - D d = 2 , 34 °
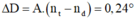
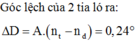
A B C I 60 60 r i'
Câu này mình nghĩ nó sẽ không có trong đề thi đâu. Liên quan đến hiện tượng khúc xạ và phản xạ toàn phần lớp 11.
Áp dung: \(\sin i=n\sin r\Rightarrow\sin r=\frac{\sin60}{n}=\frac{\sqrt{3}}{2.n}\)(1)
Điều kiện để xảy ra phản xạ toàn phần tại mặt BC là \(i'>i_{gh}\)
\(\sin i_{gh}=\frac{1}{n}\)(2)
Từ hình vẽ ta thấy: \(i'=r+30\)
\(\Rightarrow\sin i'=\sin\left(r+30\right)=\sin r\cos30+\sin30.\cos r=\frac{\sqrt{3}}{2n}.\frac{\sqrt{3}}{2}+\frac{1}{2}\sqrt{\frac{4n^2-3}{4n^2}}\)
\(\Rightarrow\sin i'>\frac{3}{4n}+\frac{1}{2}\sqrt{\frac{1}{4n^2}}=\frac{4}{4n}=\frac{1}{n}=\sin i_{gh}\)
\(\Rightarrow i'>i_{gh}\)
Như vậy, tia tới BC bị phản xạ toàn phần, và khi đến AC do tính đối xứng nên sẽ ló ra ngoài theo phương // với BC.
Đáp án B