Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

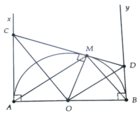
a, HS tự chứng minh
b, ΔCOD và ΔAMB đồng dạng => MC.MD = O M 2
c, AC = R 3
BD.AC = MC.MD = O M 2
=> BD = R 3 3

Theo tính chất hai tiếp tuyến cắt nhau ta có
a) ^COD=^O22 +^O32 =12 (^O1+^O2+^O3+^O4)=12 .180∘=90∘.
b) CD = CM + MD = CA + DB.
c) AC.BD=MC.MD=OM2AC.BD=MC.MD=OM2 (cố định).

a: Xét (O) có
CM,CA là tiếp tuyến
DO đó: CM=CA và OC là phân giác của góc AOM
=>C nằm trên đường trung trực của MA(1)
Ta có: OA=OM
=>O nằm trên đường trung trực của MA(2)
từ (1) và (2) suy ra CO là đường trung trực của MA
OC là phân giác của góc AOM
=>\(\widehat{AOM}=2\cdot\widehat{MOC}\)
Xét (O) có
DM,DB là tiếp tuyến
Do đó: DM=DB và OD là phân giác của góc MOB
DM=DB
nên D nằm trên đường trung trực của BM(3)
OM=OB
=>O nằm trên đường trung trực của BM(4)
Từ (3) và (4) suy ra OD là là đường trung trực của BM
Ta có: OD là phân giác của góc MOB
=>\(\widehat{MOB}=2\cdot\widehat{MOD}\)
Ta có: \(\widehat{MOA}+\widehat{MOB}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{MOC}+2\cdot\widehat{MOD}=180^0\)
=>\(2\cdot\left(\widehat{MOC}+\widehat{MOD}\right)=180^0\)
=>\(2\cdot\widehat{COD}=180^0\)
=>\(\widehat{COD}=90^0\)
Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
Xét tứ giác OACM có
\(\widehat{OAC}+\widehat{OMC}=90^0+90^0=180^0\)
=>OACM là tứ giác nội tiếp
=>\(\widehat{OAM}=\widehat{OCM}\)
Xét ΔCOD vuông tại O và ΔAMB vuông tại M có
\(\widehat{OCD}=\widehat{MAB}\)(cmt)
Do đó: ΔCOD đồng dạng với ΔAMB
b: Xét ΔOCD vuông tại O có OM là đường cao
nên \(MC\cdot MD=OM^2\)
=>\(MC\cdot MD=R^2\) không đổi khi M di chuyển trên (O)
c: AB=2R
=>OA=OB=AB/2=R
Ta có: ΔCAO vuông tại A
=>\(CA^2+AO^2=CO^2\)
=>\(CA^2+R^2=\left(2R\right)^2\)
=>\(CA^2=3R^2\)
=>\(CA=R\sqrt{3}\)
\(MC\cdot MD=R^2\)
mà MC=AC và DM=DB
nên \(AC\cdot BD=R^2\)
=>\(BD\cdot R\sqrt{3}=R^2\)
=>\(BD=\dfrac{R}{\sqrt{3}}\)
Chọn B
Cảm ơn ạ