Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trong 15 phút , mũi kim phút vạch cung tròn có số đo \(\frac{\pi}{2}.1,75\approx2,75\left(m\right)\) và mũi kim giờ vạch cung tròn có số đo \(\frac{\pi}{24}\)nên cung đó có độ dài là \(\frac{\pi}{24}.1,26\approx0,16\left(m\right)\)
tại sao lại là \(\frac{\pi}{2}\) và \(\frac{\pi}{24}\) hả bn ?

Chọn A.
Trong 30 phút mũi kim giờ chạy trên đường tròn có bán kính 10,57 cm và đi được cung có số đo là π/24
Do đó; độ dài đoạn đường mũi kim giờ đi được là ![]() .
.

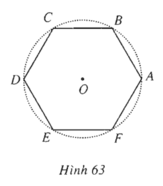
Sđ cung AB = π/3 + k2π, k ∈ Z
Sđ cung AC = 2π/3 + k2π, k ∈ Z
Sđ cung AD = π + k2π, k ∈ Z
Sđ cung AE = 4π/3 + k2π, k ∈ Z
Sđ cung AF = 5π/3 + k2π, k ∈ Z

Suy luận: Cung AB ngược hướng dương của đường tròn lượng giác nên có số đo âm, còn DA và EA có số đo dương. Do đó các phương án A, C, D bị loại.
Đáp án: B

TenAnh1
TenAnh1
A = (-4.34, -5.96)
A = (-4.34, -5.96)
A = (-4.34, -5.96)
B = (11.02, -5.96)
B = (11.02, -5.96)
B = (11.02, -5.96)
D = (10.28, -5.54)
D = (10.28, -5.54)
D = (10.28, -5.54)
F = (9.98, -5.84)
F = (9.98, -5.84)
F = (9.98, -5.84)
H = (10.64, -5.76)
H = (10.64, -5.76)
H = (10.64, -5.76)
I = (-4.38, -5.94)
I = (-4.38, -5.94)
I = (-4.38, -5.94)
J = (10.98, -5.94)
J = (10.98, -5.94)
J = (10.98, -5.94)
L = (10.42, -6.1)
L = (10.42, -6.1)
L = (10.42, -6.1)
N = (10.76, -6)
N = (10.76, -6)
N = (10.76, -6)
O = (-4.3, -5.82)
O = (-4.3, -5.82)
O = (-4.3, -5.82)
P = (11.06, -5.82)
P = (11.06, -5.82)
P = (11.06, -5.82)
R = (10.96, -5.94)
R = (10.96, -5.94)
R = (10.96, -5.94)
Dễ thấy

11. Độ dài:
\(8,43.3,85=32,4555\left(cm\right)\)
12.
Trong 30' kim giờ vạch được 1 góc \(\frac{\pi}{12}\) (rad)
\(\Rightarrow\) Độ dài cung tròn: \(\frac{\pi}{12}.10,57=2,77\left(cm\right)\)
13.
\(sin^2x.tan^2x+4sin^2x+3cos^2x\)
\(=sin^2x.tan^2x+sin^2x+3=sin^2x\left(tan^2x+1\right)+3\)
\(=\frac{sin^2x}{cos^2x}+3=tan^2x+3\)
Bạn ghi sai đề, đề đúng phải là \(sin^2x.cot^2x+4sin^2x+3cos^2x\) biểu thức này bằng 4

Trong 15 phút, mũi kim phút vạch cung tròn có số đo \(\dfrac{\pi}{2}rad\) nên cung đó có độ dài là:
\(\dfrac{\pi}{2}.1,75\) \(\approx2,75\left(m\right)\)