TV
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TN
1 tháng 10 2016
a) 4x2+3y2-4x+30y+78
=4x2-4x+1+3y2+30y+75+2
=(4x2-4x+1)+3(y2+10y+25)+2
=(2x-1)2+3(y+5)2+2>0 với mọi x
=>ko có x;y nào thỏa mãn
b)3x2+6y2-12x-20y+40
\(=3\left(x^2-4x+4\right)+6\left(y^2-\frac{10}{3}+\frac{25}{9}\right)+\frac{34}{3}\)
\(=3\left(x-2\right)^2+6\left(y-\frac{5}{3}\right)^2+\frac{34}{3}>0\) với mọi x
=>ko có x;y nào thỏa mãn
ML
11 tháng 8 2015
bạn c/m cho nó lớn hơn hoặc nhỏ hơn 0 đi mk ngại làm vì hơi nhìu ^.^ sory
25 tháng 8 2016
bài này chỉ có hsg như tui, alibaba nguyễn, hoàng lê bảo ngọc ..... làm dc
TN
1
25 tháng 1 2024
\(4x^2+3y^2-4x+30y+78=0\)
=>\(\left(4x^2-4x+1\right)+3\left(y^2+10y+25\right)+2=0\)
=>\(\left(2x-1\right)^2+3\left(y+5\right)^2+2=0\)(vô lý)
=>\(\left(x,y\right)\in\varnothing\)
T
31 tháng 7 2019
Làm lần lượt nha!
a) Ta có:
\(A=3x^2+y^2+10x-2xy+26\)
\(=\left(x^2+2xy+y^2\right)+\left(2x^2+10x+\frac{50}{4}\right)+\frac{27}{2}\)
\(=\left(x+y\right)^2+2\left(x^2+2.x.\frac{5}{2}+\frac{25}{4}\right)+\frac{27}{2}\)
\(=\left(x+y\right)^2+2\left(x+\frac{5}{2}\right)^2+\frac{27}{2}\ge\frac{27}{2}>0\) với mọi x nên nó vô nghiệm
HP
22 tháng 6 2016
\(\left(a^2+b^2\right)\left(x^2+y^2\right)=\left(ax+by\right)^2\)
\(=>a^2\left(x^2+y^2\right)+b^2\left(x^2+y^2\right)=\left(ax\right)^2+2axby+\left(by\right)^2\)
\(=>a^2x^2+a^2y^2+b^2x^2+b^2y^2-a^2x^2-2axby-b^2y^2=0\)
\(=>a^2y^2+b^2x^2-2axby=0=>\left(ay-bx\right)^2=0\)
=>ax-by=0=>ax=by
Vậy .....................
HP
22 tháng 6 2016
2) b)
Xét hiệu :
\(100^2+103^2+105^2+94^2-\left(101^2+98^2+96^2+107^2\right)\)
\(=100^2+103^2+105^2+94^2-101^2-98^2-96^2-107^2\)
\(=\left(100^2-98^2\right)+\left(103^2-101^2\right)-\left(107^2-105^2\right)-\left(96^2-94^2\right)\)
\(=\left(100-98\right)\left(100+98\right)+\left(103-101\right)\left(103+1\right)-\left(107-105\right)\left(107+105\right)\)\(-\left(96-94\right)\left(96+94\right)\)
\(=2.198+2.204-2.212-2.190=2\left(198+204-212-190\right)=2.0=0\)
Vậy 1002+1032+1052+942=1012+982+962+1072
LD
1
2 tháng 2 2022
a: \(VT=x^2+2\cdot x\cdot\dfrac{1}{2}y+\dfrac{1}{4}y^2+\dfrac{3}{4}y^2+1\)
\(=\left(x+\dfrac{1}{2}y\right)^2+\dfrac{3}{4}y^2+1>0\forall x,y\)
c: \(VT=x^2-6xy+9y^2+4x^2-4x+1+y^2-2y+1+1\)
\(=\left(x-3y\right)^2+\left(2x-1\right)^2+\left(y-1\right)^2+1>0\forall x,y\)
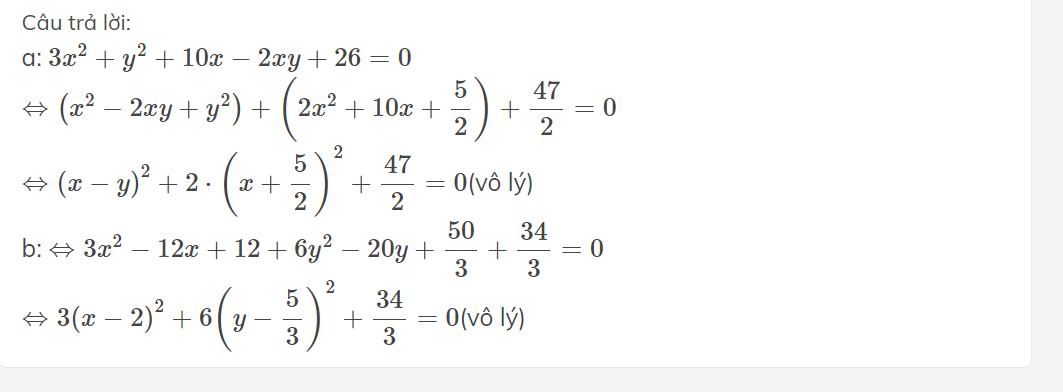
\(4x^2+3y^2-4x+30y+78\)
\(=\left(2x\right)^2-2\cdot2x\cdot1+1^2+3y^2+30y+75+2\)
\(=\left(2x-1\right)^2+3\left(y^2+2\cdot y\cdot5+5^2\right)+2\)
\(=\left(2x-1\right)^2+3\left(y+5\right)^2+2\ge2>0\)
=> đẳng thức ko thể bằng 0
=> đpcm
\(4x^2+3y^2-4x+30y+78=0\)
\(=4x^2-4x+1+3y^2+30y+75+2\)
\(=(4x^2-4x+1)+3(y^2+10y+25)+2\)
\(=(2x-1)^2+3(y+5)^2+2>0\)với mọi x
=> không có x,y nào thỏa mãn
P/S : Bài này chứng minh hay sao?