K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
A
1
21 tháng 7 2021
\(A=x^2+\frac{4}{x^2+1}\)
\(=x^2+1+\frac{4}{x^2+1}-1\)
Áp dụng bất đẳng thức cauchy cho 2 số dương x^2 + 1 và 4 / x^2 + 1
\(x^2+1+\frac{4}{x^2+1}\ge2\sqrt{\left(x^2+1\right)\cdot\frac{4}{x^2+1}}\)
\(x^2+1+\frac{4}{x^2+1}\ge4\)
\(x^2+1+\frac{4}{x^2+1}-1\ge3\)
\(A\ge3\)
Dấu = xảy ra khi và chỉ khi
\(x^2+1=\frac{4}{x^2+1}\)
\(\left(x^2+1\right)^2=4\)
\(\orbr{\begin{cases}x^2+1=2\\x^2+1=-2\end{cases}}\)
\(\orbr{\begin{cases}x^2=1\\x^2=-3\left(sai\right)\end{cases}}\)
\(\orbr{\begin{cases}x=1\\x=-1\end{cases}}\)
Vậy A > 3 khi x khác 1 và - 1
A = 3 khi x = 1 hay x = - 1
A < 3 vô nghiệm
FG
0
20 tháng 7 2021
\(a,\frac{1}{1+a}+\frac{1}{1+b}\ge\frac{4}{2+a+b}\)( BĐT cô-si dạng engel)
\(\frac{4}{2+a+b}\le\frac{4}{2+2\sqrt{ab}}=\frac{2}{1+\sqrt{ab}}=VP\)(bđt tương đương)
vậy cả hai bđt dấu "=" xảy ra đồng thời
\(\hept{\begin{cases}\frac{1}{1+a}=\frac{1}{1+b}\\a=b=1\end{cases}}\)
vậy \(\frac{1}{1+a}+\frac{1}{1+b}=\frac{2}{1+\sqrt{ab}}\)khi \(a=b=1\)
\(b,\)\(\frac{1}{1+a}+\frac{1}{1+b}>\frac{2}{1+\sqrt{ab}}\)khi và chỉ khi bđt cô -si không xảy ra dấu bằng
và bđt tương đương xảy ra dấu bằng
\(\hept{\begin{cases}\frac{1}{1+a}+\frac{1}{1+b}>\frac{4}{2+a+b}\\\frac{4}{2+a+b}=\frac{2}{1+\sqrt{ab}}\end{cases}}\)
\(\hept{\begin{cases}\frac{2+a+b}{1+a+b+ab}>\frac{4}{2+a+b}\\4+4\sqrt{ab}=4+2a+2b\end{cases}}\)
\(\hept{\begin{cases}4+a^2+b^2+4a+4b+2ab>4+4a+4a+4ab\\2\sqrt{ab}=a+b\end{cases}}\)
\(\hept{\begin{cases}a^2+b^2>2ab\\a^2+b^2=0\end{cases}}\)
\(0>2ab\)
\(ab< 0\)
rồi chia ra từng TH
ra đc \(TH1:\hept{\begin{cases}a< 0\\b>0\end{cases}}\)
\(TH2:\hept{\begin{cases}a>0\\b< 0\end{cases}}\)
\(c,\frac{1}{1+a}+\frac{1}{1+b}\ge\frac{2}{1+\sqrt{ab}}\)khi và chỉ khi
bđt cô- si dạng engel lớn hơn hoặc bằng còn bđt tương đương thì dấu bằng xảy ra
\(\hept{\begin{cases}\frac{1}{1+a}+\frac{1}{1+b}\ge\frac{4}{2+a+b}\\\frac{4}{2+a+b}=\frac{2}{1+\sqrt{ab}}\end{cases}}\)
\(\hept{\begin{cases}a^2+b^2\ge2ab\\a^2+b^2=0\end{cases}}\)
\(< =>0\ge2ab\)
vì đề bài cho \(a,b>0\)lên dấu bằng không xảy ra
vậy không có giá trị a,b nào thỏa mãn \(\frac{1}{1+a}+\frac{1}{1+b}\ge\frac{2}{1+\sqrt{ab}}\)
câu d lập luận như các câu trên cậu làm nốt nha
22 tháng 3 2021
1) a2 - ab + b2 ≥ 0
<=> ( 4a2 - 4ab + b2 ) + 3b2 ≥ 0
<=> ( 2a - b )2 + 3b2 ≥ 0 ( đúng ∀ a,b )
Vậy bđt ban đầu được chứng minh
Đẳng thức xảy ra <=> a = b = 0
2) a2 - ab + b2 ≥ 1/4( a + b )2
<=> 4a2 - 4ab + 4b2 ≥ a2 + 2ab + b2
<=> 4a2 - 4ab + 4b - a2 - 2ab - b2 ≥ 0
<=> 3a2 - 6ab + 3b2 ≥ 0
<=> a2 - 2ab + b2 ≥ 0
<=> ( a - b )2 ≥ 0 ( đúng ∀ a,b )
Vậy bđt ban đầu được chứng minh
Đẳng thức xảy ra <=> a = b
22 tháng 4 2016
1 + 1 = 3 vì:
1 + 1 = 1 đôi = 1 + 2 (đôi là 2) = 3
Cách này mình tự chế thôi, còn cách khác nữa:
Bạn đếm ngón tay là biết
1 ngón tay là 1, dấu cộng ở khe ngón tay, thêm ngón tay nữa là 2, dấu bằng ở khe ngón tay là ra ngón thứ 3
=> 1 + 1 = 3
PN
11 tháng 8 2020
nếu trong biểu thức thì viết như này , còn trình bày thì anh kid đã làm rồi
a, \(đk:x>2\)
b, \(đk:x\ge0;x\ne9\)
10 tháng 8 2020
a)
Các biểu thức sau có nghĩa khi \(\frac{1}{x^2-4}>0;x^2-4\ne0\Rightarrow x>2\)
b)
Biểu thức có nghĩa khi \(x\ge0;x\ne9\)
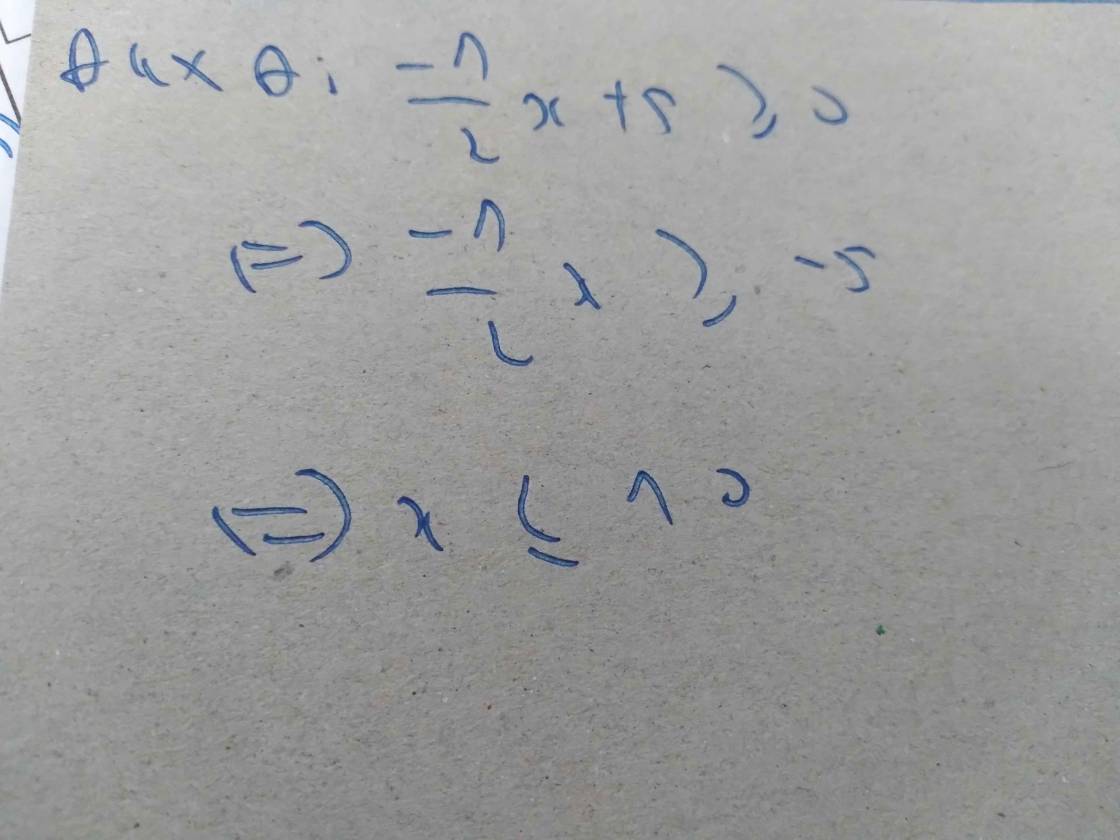
dấu trừ biến thành dấu cộng
khi hiệu biến thành số bị chia
5-4=1
2-1=1
Khi dấu trừ biến thành dấu cộng
4+1=5
1+1=2