
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(x-3\right)^2+\left|y^2-9\right|=0\)
Vì \(\left\{{}\begin{matrix}\left(x-3\right)^2\ge0\forall x\\\left|y^2-9\right|\ge0\forall y\end{matrix}\right.\)
để bt = 0 \(\Leftrightarrow\left\{{}\begin{matrix}\left(x-3\right)^2=0\\\left|y^2-9\right|=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3=0\\y^2-9=0\Rightarrow y^2=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3\\\left[{}\begin{matrix}y=3\\y=-3\end{matrix}\right.\end{matrix}\right.\)
Vậy.....
\(\left(x-3\right)^2+\left|y^2-9\right|=0\)
\(\Rightarrow\left[{}\begin{matrix}\left(x-3\right)^2=0\\\left|y^2-9\right|=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x-3=0\\y^2-9=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\y^2=9\left[{}\begin{matrix}y=3\\y=-3\end{matrix}\right.\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x=3\\y=3hoặcy=-3\end{matrix}\right.\)

\(x-y=9\Rightarrow x=9+y\Rightarrow y=x-9\)
Ta có:
\(\dfrac{4x-9}{3x+y}-\dfrac{4y+9}{3y+x}\)
\(=\dfrac{3x+x-9}{3x+y}-\dfrac{3y+y+9}{3y+x}\)
\(=\dfrac{3x+\left(x-9\right)}{3x+y}-\dfrac{3y+\left(y+9\right)}{3y+x}\)
\(=\dfrac{3x+y}{3x+y}-\dfrac{3y+x}{3y+x}\)
\(=1-1\)
\(=0\)
Vậy biểu thức \(\dfrac{4x-9}{3x+y}-\dfrac{4y+9}{3y+x}\)khi \(x-y=9\) là 0
\(x-y=9\Rightarrow y=x-9\) thay vào biểu thức B ta được :
\(B=\dfrac{4x-9}{3x+\left(x-9\right)}-\dfrac{4\left(x-9\right)+9}{3\left(x-9\right)+x}=\dfrac{4x-9}{4x-9}-\dfrac{4x-27}{4x-27}=1-1=0\)
Vậy giá trị của B là 0 tại \(x-y=9\)

\(\left(x-3\right).\left(x-2015\right)< 0\)
\(\Rightarrow\left(x-3\right)và\left(x-2015\right)\) phải khác dấu
\(\Rightarrow\left(x-3\right)< \left(x-2015\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x-3>0\\x-2015< 0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x>3\\x< 2015\end{matrix}\right.\)
\(\Rightarrow3< x< 2015\)
\(\Rightarrow x\in\left\{4;5;6;7;8;...;2013;2014\right\}\)
( ko bt đúng hay sai nx )
thám tử
\(\left(x-3\right)\left(x-2015\right)< 0\)
Với mọi \(x\in R\) thì:
\(x-2015< x-3\)
Khi đó: \(\left\{{}\begin{matrix}x-2015< 0\\x-3>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< 2015\\x>3\end{matrix}\right.\)
Nên \(3< x< 2015\)

Với mọi x ta có:
|x - 2001| = |2001 - x|
=> A = |x - 2002| + |2001 - x|
Với mọi x ta cũng có:
|x - 2002| + | 2001 - x| \(\ge\)|(x - 2002) + (2001 - x)|
A \(\ge\) |1|
A \(\ge\) 1
Dấu bằng xảy ra <=> (x - 2002).(2001 - x) \(\ge\) 0
=> x - 2002 \(\ge\) 0; 2001 - x \(\ge\) 0 (1)
hoặc x - 2002 \(\le\) 0; 2001 - x \(\le\) 0 (2)
Từ (1) => x > hoặc = 2002; x < hoặc = 2001 => x không có giá trị thoả mãn
Từ (2) => x < hoặc = 2002 ; x > hoặc = 2001 => 2001 \(\le\) x \(\le\) 2002
Vậy 2001 \(\le\) x \(\le\) 2002 thì A có giá trị nhỏ nhất = 1

>> Mình không chép lại đề bài nhé ! <<
Cách 1 :
\(A=\left(\dfrac{36-4+3}{6}\right)-\left(\dfrac{30+10-9}{6}\right)-\left(\dfrac{18-14+15}{6}\right)=\dfrac{35}{6}-\dfrac{31}{6}-\dfrac{19}{6}=-\dfrac{15}{6}=-\dfrac{5}{2}\)
Cách 2 :
\(A=6-\dfrac{2}{3}+\dfrac{1}{2}-5+\dfrac{5}{3}-\dfrac{3}{2}-3-\dfrac{7}{3}+\dfrac{5}{2}\)
\(A=\left(6-5-3\right)-\left(\dfrac{2}{3}+\dfrac{5}{3}-\dfrac{7}{3}\right)+\left(\dfrac{1}{2}+\dfrac{3}{2}-\dfrac{5}{2}\right)\)
\(A=-2-0-\dfrac{1}{2}=-\dfrac{5}{2}\)
Cách 1 :
\(\left(6-\dfrac{2}{3}+\dfrac{1}{2}\right)-\left(5+\dfrac{5}{3}-\dfrac{3}{2}\right)-\left(3-\dfrac{7}{3}+\dfrac{5}{2}\right)\)
\(=\left(\dfrac{36}{6}-\dfrac{4}{6}+\dfrac{3}{6}\right)-\left(\dfrac{30}{6}+\dfrac{10}{6}-\dfrac{9}{6}\right)-\left(\dfrac{18}{6}-\dfrac{14}{6}+\dfrac{15}{6}\right)\)
\(=\dfrac{35}{6}-\dfrac{31}{6}-\dfrac{19}{6}\)
\(=-\dfrac{5}{2}\)
Cách 2 :
\(\left(6-\dfrac{2}{3}+\dfrac{1}{2}\right)-\left(5+\dfrac{5}{3}-\dfrac{3}{2}\right)-\left(3-\dfrac{7}{3}+\dfrac{5}{2}\right)\)
\(=6-\dfrac{2}{3}+\dfrac{1}{2}-5-\dfrac{5}{3}+\dfrac{3}{2}-3+\dfrac{7}{3}-\dfrac{5}{2}\)
\(=\left(6-5-3\right)+\left(\dfrac{-2}{3}+\dfrac{-5}{3}+\dfrac{7}{3}\right)+\left(\dfrac{1}{2}+\dfrac{3}{2}+\dfrac{-5}{2}\right)\)
\(=\left(-2\right)+0+\dfrac{-1}{2}\)
\(=\dfrac{-5}{2}\)

Ta có: \(\left|x-1\right|+\left|x-5\right|=\left|x-1\right|+\left|5-x\right|\)
Nhận thấy: \(\left[{}\begin{matrix}\left|x-1\right|\ge x-1\\\left|5-x\right|\ge5-x\end{matrix}\right.\)
\(\Rightarrow\left|x-1\right|+\left|5-x\right|\ge x-1+5-x\)
\(\Rightarrow\left|x-1\right|+\left|5-x\right|\ge4\)
Dấu \("="\) xảy ra khi:
\(\left[{}\begin{matrix}x-1\ge0\\5-x\ge0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x\ge1\\x\le5\end{matrix}\right.\) \(\Rightarrow1\le x\le5\)
Vậy \(1\le x\le5.\)
Cho mk thêm cái ạ:
\(x\in\left\{1;2;3;4;5\right\}\)
Vậy \(x\in\left\{1;2;3;4;5\right\}\)

Ta có :
\(S=1.2+2.3+...+49.50\)
\(\Leftrightarrow3S=1.2.\left(3-0\right)+2.3.\left(4-1\right)+...+49.50.\left(51-48\right)\)
\(\Leftrightarrow3S=1.2.3-0.1.2+2.3.4-1.2.3+...+49.50.51-48.49.50\)
\(\Leftrightarrow3S=49.50.51\)
\(\Leftrightarrow S=\frac{49.50.51}{3}=41650\)
S=1 . 2 + 2.3+3.4+.....+49.100
3S=1.2.3+2.3.3+3.4.3+....+49.50.3
3S=1.2.3+2.3.(4-1)+3.4(5-2)+....+49.50(51-48)
3S=1.2.3-2.3.4+2.3.4-2.3.1+......+48.49.50+49.50.51
3S=49.50.51
S=49.50.51 / 3
S=41650
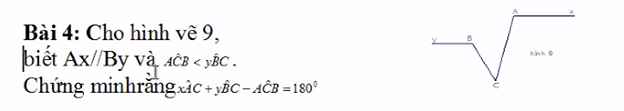 cần gấp ae ưi
cần gấp ae ưi
