K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
2 tháng 3 2017
Ta có: \(\left|x-1\right|+\left|x-5\right|=\left|x-1\right|+\left|5-x\right|\)
Nhận thấy: \(\left[{}\begin{matrix}\left|x-1\right|\ge x-1\\\left|5-x\right|\ge5-x\end{matrix}\right.\)
\(\Rightarrow\left|x-1\right|+\left|5-x\right|\ge x-1+5-x\)
\(\Rightarrow\left|x-1\right|+\left|5-x\right|\ge4\)
Dấu \("="\) xảy ra khi:
\(\left[{}\begin{matrix}x-1\ge0\\5-x\ge0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x\ge1\\x\le5\end{matrix}\right.\) \(\Rightarrow1\le x\le5\)
Vậy \(1\le x\le5.\)
2 tháng 3 2017
Cho mk thêm cái ạ:
\(x\in\left\{1;2;3;4;5\right\}\)
Vậy \(x\in\left\{1;2;3;4;5\right\}\)
MS
0
LC
2
T
15 tháng 3 2017
2.
a) +) ta co: tam giác GLO
GL = 6, LO = 8, OG = 10
=> GL < LO < GO ( 6<8<10)
=> góc O < góc G < góc L ( quan hệ giữa góc và cạnh đối diện trong tam giác LOG )
+) ta co: tam giac UVW
góc V = 40, góc U = 50
=> góc W = 180 - ( góc V + goc Ư )
= 180 - ( 50 + 40)
= 90
=> góc V < góc U < góc W
=> UW < VW < VU ( quan hệ giữa cạnh và góc trong tam giác ACB )
23 tháng 4 2017
Giải:
Do \(\left(2016a+13b-1\right)\left(2016^a+2016a+b\right)\) \(=2015\)
Nên \(2016a+13b-1\) và \(2016^a+2016a+b\) là 2 số lẻ \((*)\)
Ta xét 2 trường hợp:
Trường hợp 1: Nếu \(a\ne0\) thì \(2016^a+2016a\) là số chẵn
Do \(2016^a+2016a+b\) lẻ \(\Rightarrow b\) lẻ
Với \(b\) lẻ \(\Rightarrow13b-1\) chẵn do đó \(2016a+13b-1\) chẵn (trái với \((*)\))
Trường hợp 2: Nếu \(a=0\) thì:
\(\left(2016.0+13b-1\right)\left(2016^0+2016.0+b\right)\) \(=2015\)
\(\Leftrightarrow\left(13b-1\right)\left(b+1\right)=2015=1.5.13.31\)
Do \(b\in N\Rightarrow\left(13b-1\right)\left(b+1\right)=5.403=13.155\) \(=31.65\)
Và \(13b-1>b+1\)
\(*)\) Nếu \(b+1=5\Rightarrow b=4\Rightarrow13b-1=51\) (loại)
\(*)\) Nếu \(b+1=13\Rightarrow b=12\Rightarrow13b-1=155\) (chọn)
\(*)\) Nếu \(b+1=31\Rightarrow b=30\Rightarrow13b-1=389\) (loại)
Vậy \(\left(a,b\right)=\left(0;12\right)\)
LT
4
29 tháng 8 2017
lê tiến trường
\(\left|x-564\right|=532\)
\(\Rightarrow\left[{}\begin{matrix}x-564=532\\x-564=-532\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=532+564=1096\\x=\left(-532\right)+564=32\end{matrix}\right.\)
Vậy x = 1096 và x = 32
29 tháng 8 2017
TH1: x-564=532
x= 532+564
x= 1098
TH2: x-564=-532
x= -532+564
x= 34
X thuộc( phải bằng dau) \(\left\{34,1098\right\}\)
19 tháng 3 2017
Ta có:\(2009^{20}=\left(2009^2\right)^{10}=4036081^{10}< 20092009^{10}\)
Vậy \(2009^{20}< 20092009^{10}\)
MD
2
19 tháng 4 2017
B=\(\left(\dfrac{2012}{x^2}\right)+4x+2013\) hay B=\(\left(\dfrac{2012}{x}\right)^2+4x+2013\) vậy bn
19 tháng 4 2017
A=\(\left(-x\right)^2+3x+4=x^2+3x+4\)
=\(x^2+3x+2,25+1,75=x^2+1,5x+1,5^2+1,75\)
=\(\left(x+1,5\right)^2+1,75\)
Thấy\(\left(x+1,5\right)^2\ge0\Rightarrow\left(x+1,5\right)^2+1,75\ge1,75\) hay \(A\ge1,75\)
Vậy GTNN của A là 1,75 khi x=-1,5
G
14 tháng 9 2017
Giải:
Theo đề ra, ta có:
\(3x=-2y\Leftrightarrow\dfrac{x}{-2}=\dfrac{y}{3}\)
Và \(2x+y=5\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{-2}=\dfrac{y}{3}=\dfrac{2x}{-4}=\dfrac{2x+y}{-4+3}=\dfrac{5}{-1}=-5\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{-2}=-5\\\dfrac{y}{3}=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-5.\left(-2\right)\\y=-5.3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=10\\y=-15\end{matrix}\right.\)
Vậy \(x=10\) và \(y=-15\).
Chúc bạn học tốt!!!
14 tháng 9 2017
\(3x=-2y\)
=>\(\dfrac{x}{-2}=\dfrac{y}{3}\)
Áp dụng tính chất của dãy tỉ số bằng nhau,ta có:
\(\dfrac{x}{-2}=\dfrac{y}{3}=\dfrac{2x+7}{2.\left(-2\right)+3}=\dfrac{5}{-1}=-5\)
=>\(x=\left(-5\right).\left(-2\right)=10\)
\(y=-5.3=-15\)
Vậy...
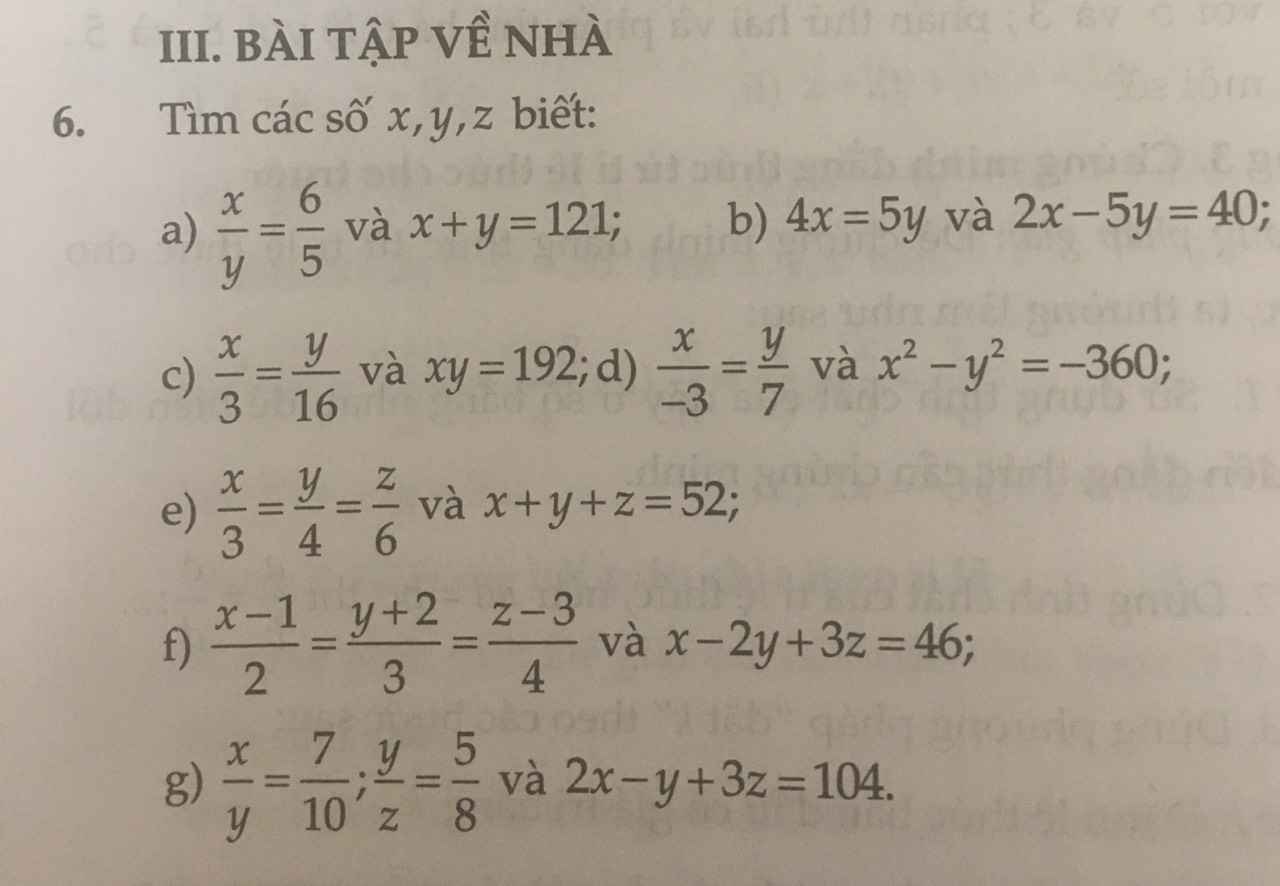
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{6}=\dfrac{y}{5}=\dfrac{x+y}{6+5}=\dfrac{121}{11}=11\)
Do đó: x=66; y=55