Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
Xác định gia tốc rơi tự do của trụ thép theo công thức:
\(g=a=\dfrac{2s}{t^2}\left(m/s^2\right)\)
2.
Để xác định gia tốc rơi tự do của trụ thép cần đo đại lượng: quãng đường rơi của trụ thép và thời gian rơi.
3.
Để trụ thép rơi qua cổng quang điện cần chú ý điều chỉnh máng thẳng đứng (quan sát dây rọi) đồng thời điều chỉnh cổng quang điện để trụ thép rơi qua cổng quang điện.
4.
Cần đặt đồng hồ đo thời gian hiện số ở chế độ \(A\leftrightarrow B\) để đo được đại lượng cần đo.

1.
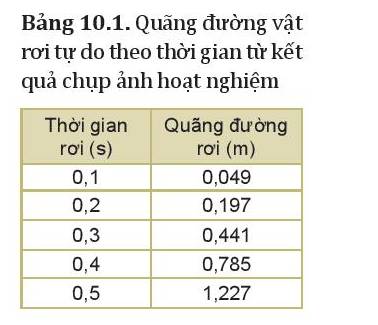
Dựa vào bảng 10.1, ta thấy rằng
+ Trong 0,1 s đầu tiên, vật đi được quãng đường là 0,049 m
+ Trong 0,1 s tiếp theo, vật đi được quãng đường là 0,197 – 0,049 = 0,148 m
+ Từ 0,2 s đến 0,3 s, vật đi được quãng đường là 0,441 – 0,197 = 0,244 m
+ Từ 0,3 s đến 0,4 s, vật đi được quãng đường là 0,785 – 0,441 = 0,344 m
+ Từ 0,4 s đến 0,5 s, vật ssi được quãng đường là 1,227 – 0,785 = 0,442 m
Thông qua các số liệu trên, ta thấy cùng trong một khoảng thời gian, quãng đường vật rơi được càng dài, chứng tỏ vật rơi tự do
2.
Gia tốc của chuyển động rơi tự do
\(a = \frac{{2s}}{{{t^2}}} = \frac{{2.0.049}}{{0,{1^2}}} = 9,8(m/{s^2})\)

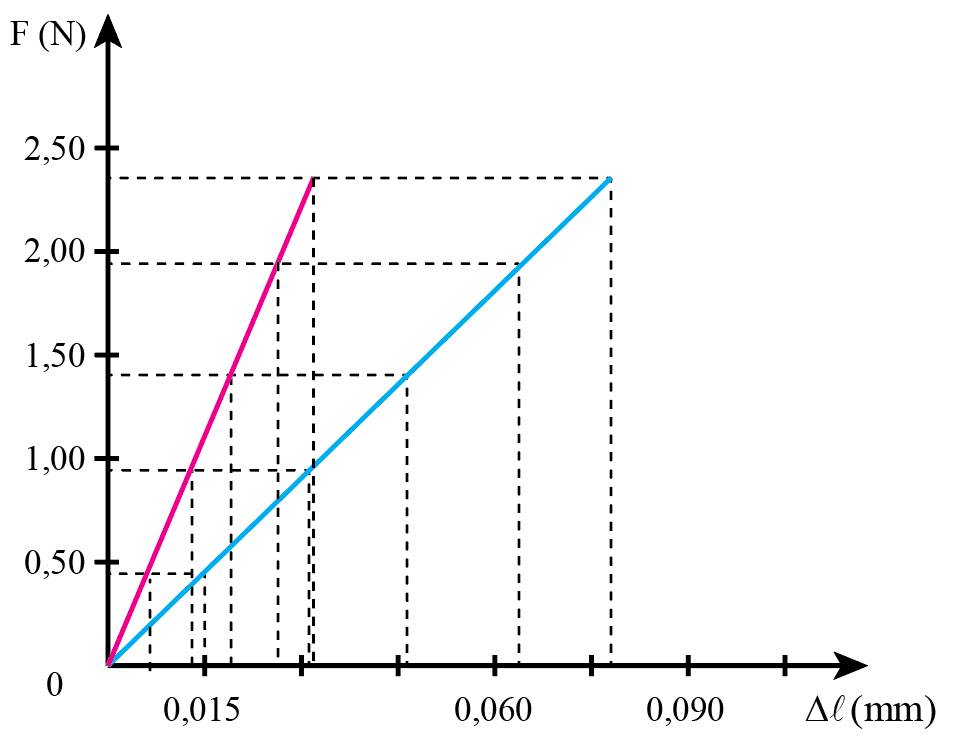
Đồ thị có dạng đường thẳng hướng lên trên, cho thấy lò xo có độ dãn tỉ lệ thuận với lực tác dụng.

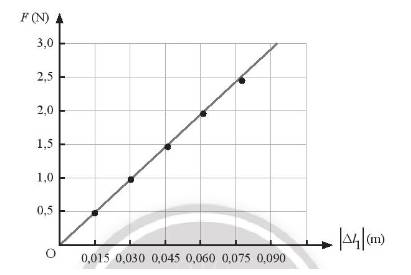
a) Đồ thị biểu diễn sự phụ thuộc vào lực đàn hồi (trục tung) vào độ biến dạng của lò xo 1 (trục hoành).
Đồ thị biểu diễn sự phụ thuộc của lực đàn hồi (trục tung) vào độ biến dạng của lò xo 2 (trục hoành).
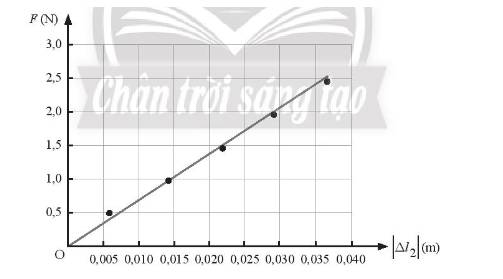
b) Đồ thị có dạng đường thẳng và đi qua gốc tọa độ (đồ thị này được vẽ dựa trên số liệu thí nghiệm được cho trong SGK). Từ đó có thể suy ra được độ lớn lực đàn hồi tỉ lệ thuận với độ biến dạng của lò xo.

Tính chất của chuyển động rơi tự do:
+ Chuyển động thẳng nhanh dần đều
+ Gia tốc của chuyển động bằng gia tốc trọng trường

Tính chất của chuyển động rơi tự do:
+ Chuyển động thẳng nhanh dần đều
+ Gia tốc của chuyển động bằng gia tốc trọng trường
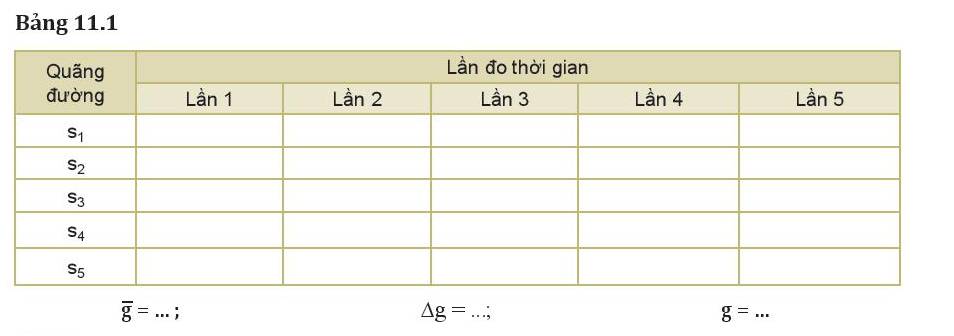

* Kết quả thí nghiệm:
1. Tính giá trị trung bình và sai số tuyệt đối của phép đo gia tốc rơi tự do
- Lần 1: \({g_1} = \frac{{2{s_1}}}{{t_1^2}} = \frac{{2.0,4}}{{0,{{285}^2}}} = 9,849(m/{s^2})\)
- Lần 2: \({g_2} = \frac{{2{s_2}}}{{t_2^2}} = \frac{{2.0,4}}{{0,{{285}^2}}} = 9,849(m/{s^2})\)
- Lần 3: \({g_3} = \frac{{2{s_3}}}{{t_3^2}} = \frac{{2.0,4}}{{0,{{285}^2}}} = 9,919(m/{s^2})\)
- Lần 4: \({g_4} = \frac{{2{s_4}}}{{t_4^2}} = \frac{{2.0,4}}{{0,{{285}^2}}} = 9,849(m/{s^2})\)
- Lần 5: \({g_5} = \frac{{2{s_5}}}{{t_5^2}} = \frac{{2.0,4}}{{0,{{286}^2}}} = 9,780(m/{s^2})\)
Gia tốc trung bình là: \(\overline g = \frac{{9,849 + 9,849 + 9,919 + 9,849 + 9,780}}{5} = 9,849(m/{s^2})\)
Sai số tuyệt đối của gia tốc trong các lần đo
\(\begin{array}{l}\Delta {g_1} = \left| {\overline g - {g_1}} \right| = \left| {9,849 - 9,849} \right| = 0\\\Delta {g_2} = \left| {\overline g - {g_2}} \right| = \left| {9,849 - 9,849} \right| = 0\\\Delta {g_3} = \left| {\overline g - {g_3}} \right| = \left| {9,849 - 9,919} \right| = 0,07\\\Delta {g_4} = \left| {\overline g - {g_4}} \right| = \left| {9,849 - 9,849} \right| = 0\\\Delta {g_5} = \left| {\overline g - {g_5}} \right| = \left| {9,849 - 9,780} \right| = 0,069\end{array}\)
Sai số tuyệt đối trung bình là: \(\overline {\Delta g} = \frac{{\Delta {g_1} + \Delta {g_2} + \Delta {g_3} + \Delta {g_4} + \Delta {g_5}}}{5} = 0,028\)
Suy ra kết quả: \(g = 9,849 \pm 0,028\)
2. Trong thí nghiệm người ta dùng trụ thép làm vật rơi nhằm mục đích khi ta thả vật rơi thì xác suất phương rơi của vật chắn tia hồng ngoại ở cổng quang điện cao, giúp ta thực hiện thí nghiệm dễ dàng hơn
- Có thể dùng vật thả rơi là viên bi thép, nhưng xác suất khi thả rơi viên bi có phương rơi không chắn được tia hồng ngoại cao hơn khi dùng trụ thép, nên khi làm thí nghiệm với viên bi ta cần căn chỉnh và thả theo đúng phương của dây rọi.