giup em voi mn ko can ve hinh dau de em tu ve cung dc a
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
18 tháng 9 2023
Em thấy bạn Vuông nói đúng
Để chứng minh điều này, ta có thể chỉ ra trường hợp 2 góc bằng nhau nhưng không đối đỉnh.
Ví dụ:
\(\widehat {{O_1}} = \widehat {{O_2}}\) nhưng hai góc này không đối đỉnh
QT
1
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)
giup em dc ko a em dang can gap a ko can ve hinh dau a
KV
11 tháng 10 2023
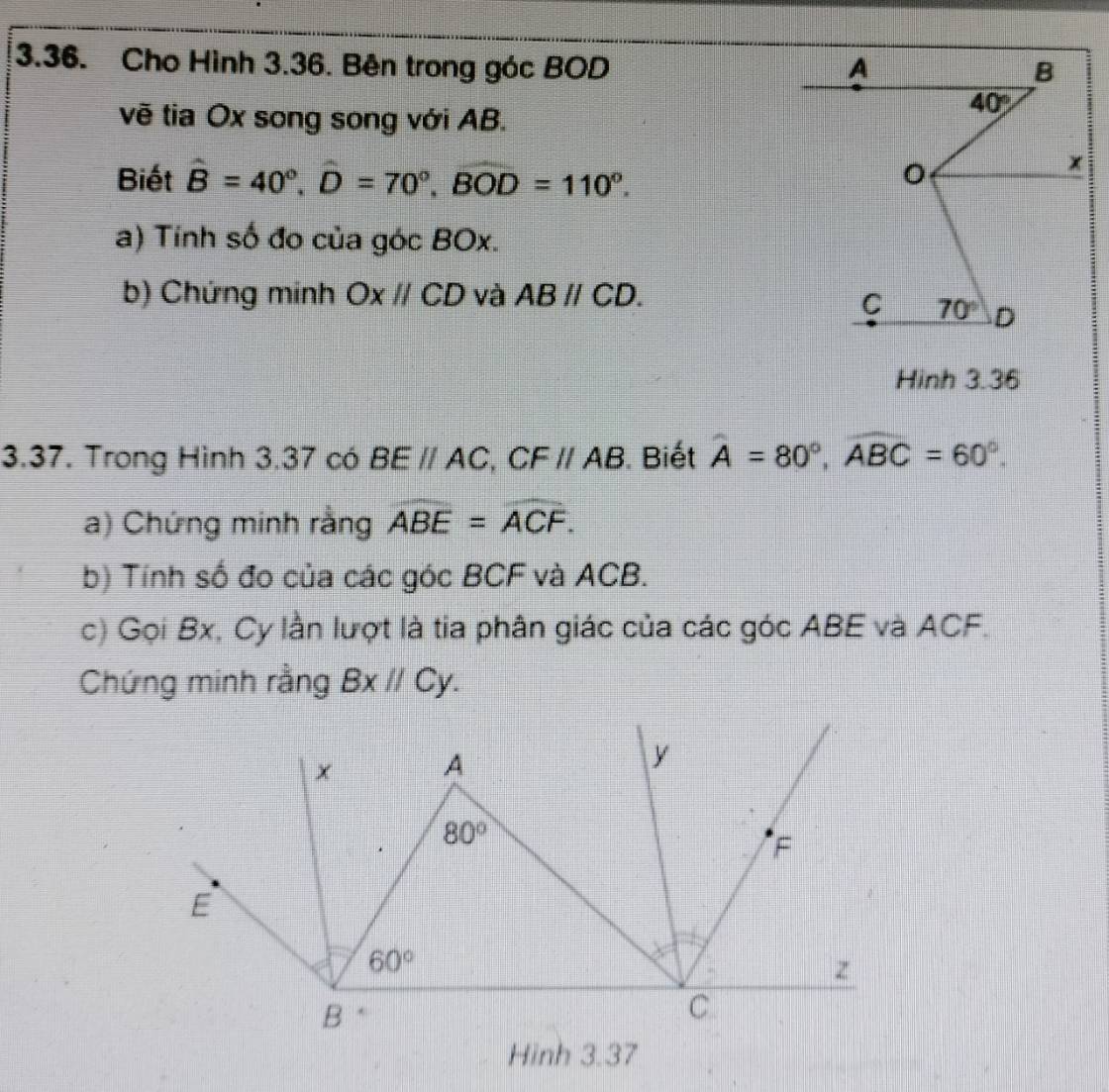
Bài 3.37
a) Do BE // AC (gt)
⇒ ∠ABE = ∠A = 80⁰ (so le trong)
Do CF // AB
⇒ ∠ACF = ∠A = 80⁰ (so le trong)
⇒ ∠ABE = ∠ACF = 80⁰
b) Do CF // AB
⇒ ∠FCz = ∠ABC = 60⁰ (đồng vị)
Ta có:
∠BCF + ∠FCz = 180⁰ (kề bù)
⇒ ∠BCF = 180⁰ - ∠FCz
= 180⁰ - 60⁰
= 120⁰
⇒ ∠ACB = ∠BCF - ∠ACF
= 120⁰ - 80⁰
= 40⁰
c) Do Bx là tia phân giác của ∠ABE
⇒ ∠ABx = ∠ABE : 2 = 80⁰ : 2 = 40⁰
⇒ ∠xBC = ∠ABx + ∠ABC
= 40⁰ + 60⁰
= 100⁰
Do Cy là tia phân giác của ∠ACF
⇒ ∠yCF = ∠ACF : 2 = 80⁰ : 2 = 40⁰
⇒ ∠yCz = ∠yCF + ∠FCz
= 40⁰ + 60⁰
= 100⁰
⇒ ∠xBC = ∠yCz = 100⁰
Mà ∠xBC và ∠yCz là hai góc đồng vị
⇒ Bx // Cy
KV
11 tháng 10 2023
Bài 3.36
a) Do Ox // AB
⇒ ∠BOx = ∠ABO = 40⁰ (so le trong)
b) Ta có:
∠xOD = ∠BOD - ∠BOx
= 110⁰ - 40⁰
= 70⁰
⇒ ∠xOD = ∠ODC = 70⁰
Mà ∠xOD và ∠ODC là hai góc so le trong
⇒ Ox // CD
Mà Ox // AB (gt)
⇒ AB // CD
QT
1
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
Đoạn thẳng đơn vị được chia thành 6 phần bằng nhau, lấy một đoạn làm đơn vị mới, đơn vị mới bằng \(\frac{1}{6}\) đơn vị cũ.
Điểm A nằm bên phải gốc O và cách O một đoạn bằng 10 đơn vị mới. Do đó điểm A biểu diễn số hữu tỉ \(\frac{{10}}{6} = \frac{5}{3}\)
Điểm B nằm bên trái gốc O và cách O một đoạn bằng 5 đơn vị mới. Do đó điểm B biểu diễn số hữu tỉ \(\frac{{ - 5}}{6}\)
Điểm C nằm bên trái gốc O và cách O một đoạn bằng 13 đơn vị mới. Do đó điểm C biểu diễn số hữu tỉ \(\frac{{ - 13}}{6}\)
KV
25 tháng 1 2024
\(5x=3y\Rightarrow x=\dfrac{3y}{5}\)
Thay \(x=\dfrac{3y}{5}\) vào biểu thức \(x^2-y^2=-4\) ta có:
\(\left(\dfrac{3y}{5}\right)^2-y^2=-4\)
\(\dfrac{9y^2}{25}-y^2=-4\)
\(-\dfrac{16}{25}y^2=-4\)
\(y^2=-\dfrac{4}{\dfrac{-16}{25}}\)
\(y^2=\dfrac{25}{4}\)
\(\Rightarrow y=-\dfrac{5}{2};y=\dfrac{5}{2}\)
*) \(y=-\dfrac{5}{2}\Rightarrow x=\dfrac{3.\left(-\dfrac{5}{2}\right)}{5}=-\dfrac{3}{2}\)
*) \(y=\dfrac{5}{2}\Rightarrow x=\dfrac{3.\dfrac{5}{2}}{5}=\dfrac{3}{2}\)
Vậy ta được các cặp giá trị \(\left(x;y\right)\) thỏa mãn:
\(\left(-\dfrac{3}{2};-\dfrac{5}{2}\right);\left(\dfrac{3}{2};\dfrac{5}{2}\right)\)
AH
Akai Haruma
Giáo viên
31 tháng 1 2024
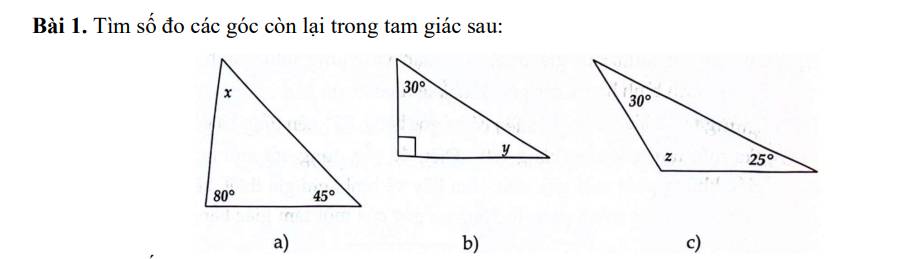
Lời giải:
Áp dụng tính chất tổng 3 góc trong một tam giác bằng $180^0$
a.
$x=180^0-80^0-45^0=55^0$
b.
$y=180^0-30^0-90^0=60^0$
c.
$z=180^0-30^0-25^0=125^0$
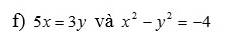
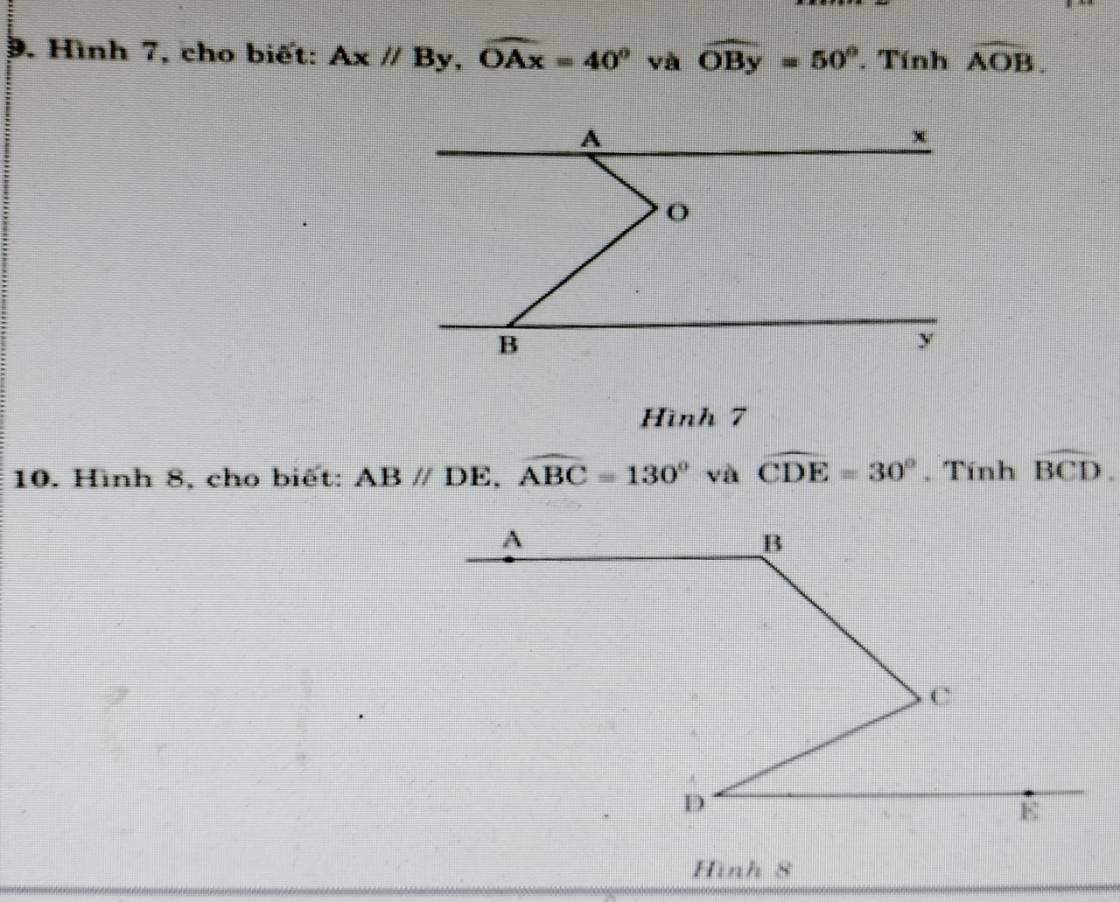
Bài 9
Qua O vẽ đường thẳng zz' // Ax // By
Do Ax // zz'
⇒ ∠AOz = ∠OAx = 40⁰
Do By // zz'
⇒ ∠zOB = ∠OBy = 50⁰ (so le trong)
⇒ ∠AOB = ∠AOz + ∠zOB
= 40⁰ + 50⁰
= 90⁰
Bài 10
Do AB // xx'
⇒ ∠ABC = ∠BCx' = 130⁰ (so le trong)
Ta có:
∠BCx + ∠BCx' = 180⁰ (kề bù)
⇒ ∠BCx = 180⁰ - ∠BCx'
= 180⁰ - 130⁰
= 50⁰
Do DE // xx'
⇒ ∠xCD = ∠CDE = 30⁰ (so le trong)
⇒ ∠BCD = ∠BCx + ∠xCD
= 50⁰ + 30⁰
= 80⁰