
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\left(m-2;6\right),B=\left(-2;2m+2\right).\)
Để \(A,B\ne\varnothing\)
\(\Rightarrow\orbr{\begin{cases}m-2\ge-2\\2m+2>6\end{cases}}\Rightarrow\orbr{\begin{cases}m\ge0\\m>2\end{cases}}\)
Kết hợp ĐK \(2< m< 8\)
\(\Rightarrow m\in\left(2;8\right)\)

a ) \mathbb{R} \backslash (-3; \, 1]R\(−3;1]=(-∞;-3]∪(1;+∞)
b) (-\infty; \, 1) \backslash [-2; \, 0](−∞;1)\[−2;0]=(- (-\infty; \, 1) \backslash [-2; \, 0]∞;-2)∪(0;1)

a) \(B\subset A\)
\(\Rightarrow\left(-4;5\right)\subset\left(2m-1;m+3\right)\)
\(\Rightarrow2m-1\le-4< 5\le m+3\)
\(\Rightarrow\hept{\begin{cases}2m-1\ge4\\5\le m+3\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}m< -\frac{3}{2}\\m\ge2\end{cases}}\left(ktm\right)\)
\(\Rightarrow m\in\varnothing\)
b) \(A\text{∩ }B=\varnothing\)
\(\Rightarrow\orbr{\begin{cases}m+3< -4\\5< 2m-1\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}m< -7\\m>3\end{cases}}\)
Vậy \(m< -7;m>3\)

Vì ABCD là hình bình hành nên ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (đpcm)

Có 7 trận: Tứ kết 1, Tứ kết 2, Tứ kết 3, Tứ kết 4, Bán kết 1, Bán kết 2, Chung kết.

5.
Tọa độ dỉnh của (P) là: \(I\left(-\dfrac{b}{2a};\dfrac{-\Delta}{4a}\right)\Rightarrow I\left(1;-4m-2\right)\)
Để I thuộc \(y=3x-1\)
\(\Rightarrow-4m-2=3.1-1\)
\(\Rightarrow m=-1\)
6.a.
Với \(a\ne0\)
\(\left\{{}\begin{matrix}64a+8b+c=0\\-\dfrac{b}{2a}=5\\\dfrac{4ac-b^2}{4a}=12\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}64a+8b+c=0\\b=-10a\\4ac-b^2=48a\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}c=-64a-8b=-64a-8\left(-10a\right)=16a\\b=-10a\\4ac-b^2=48a\end{matrix}\right.\)
\(\Rightarrow4a.16a-\left(-10a\right)^2=48a\)
\(\Rightarrow a=-\dfrac{4}{3}\Rightarrow b=\dfrac{40}{3}\Rightarrow c=-\dfrac{64}{3}\)
Hay pt (P): \(y=-\dfrac{4}{3}x^2+\dfrac{40}{3}x-\dfrac{64}{3}\)
b.
Thay tọa độ 3 điểm vào pt (P) ta được:
\(\left\{{}\begin{matrix}c=-1\\a+b+c=-1\\a-b+c=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=-1\\c=-1\end{matrix}\right.\)
Pt (P): \(y=x^2-x-1\)
c.
Do (P) đi qua 3 điểm có tọa độ (1;16); (-1;0); (5;0) nên ta có:
\(\left\{{}\begin{matrix}a+b+c=16\\a-b+c=0\\25a+5b+c=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-2\\b=8\\c=10\end{matrix}\right.\)
hay pt (P) có dạng: \(y=-2x^2+8x+10\)

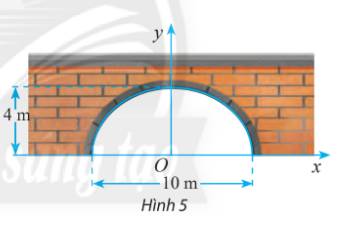
Chiều cao là 4 m tương ứng với \(b = 4\)
Chiều rộng bằng 10 m nên \(2a = 10 \Rightarrow a = 5\)
Vậy phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{16} = 1\)
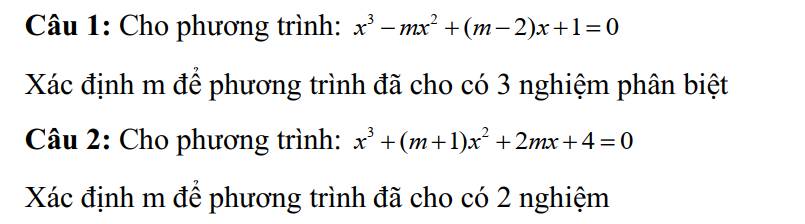 GIÚP MÌNH VỚI! HELP MEEEEEEE 😭
GIÚP MÌNH VỚI! HELP MEEEEEEE 😭


1.
\(x^3-mx^2+\left(m-2\right)x+1=0\)
\(\Leftrightarrow x^3-2x+1-m\left(x^2-x\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+x-1\right)-mx\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2-\left(m-1\right)x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x^2-\left(m-1\right)x-1=0\left(1\right)\end{matrix}\right.\)
Để pt có 3 nghiệm pb \(\Leftrightarrow f\left(x\right)=x^2-\left(m-1\right)x-1=0\) có 2 nghiệm pb khác 1
\(\Leftrightarrow f\left(1\right)=1-\left(m-1\right)-1\ne0\) (pt trên hiển nhiên luôn có 2 nghiệm pb trái dấu do \(ac=-1< 0\))
\(\Leftrightarrow m\ne1\)
2.
\(x^3+\left(m+1\right)x^2+2mx+4=0\)
\(\Leftrightarrow x^3+x^2+4+mx\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2-x+2\right)+mx\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2+\left(m-1\right)x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x^2+\left(m-1\right)x+2=0\left(1\right)\end{matrix}\right.\)
Pt có 2 nghiệm khi:
TH1: (1) có nghiệm kép khác 2
\(\Rightarrow\left\{{}\begin{matrix}\Delta=\left(m-1\right)^2-8=0\\-\dfrac{b}{2a}=\dfrac{1-m}{2}\ne2\end{matrix}\right.\) \(\Rightarrow m=1\pm2\sqrt{2}\)
TH2: (1) có 2 nghiệm pb và 1 nghiệm trong đó bằng 2
\(\Rightarrow\left\{{}\begin{matrix}\Delta=\left(m-1\right)^2-8>0\\f\left(2\right)=4+2\left(m-1\right)+2=0\end{matrix}\right.\) \(\Rightarrow m=-2\)
Em cảm ơn ạ!