Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

nHCl=0,6 mol
FeO+2HCl-->FeCl2+ H2O
x mol x mol
Fe2O3+6HCl-->2FeCl3+3H2O
x mol 2x mol
72x+160x=11,6 =>x=0,05 mol
A/ CFeCl2=0,05/0,3=1/6 M
CFeCl3=0,1/0,3=1/3 M
CHCl du=(0,6-0,4)/0,3=2/3 M
B/
NaOH+ HCl-->NaCl+H2O
0,2 0,2
2NaOH+FeCl2-->2NaCl+Fe(OH)2
0,1 0,05
3NaOH+FeCl3-->3NaCl+Fe(OH)3
0,3 0,1
nNaOH=0,6
CNaOH=0,6/1,5=0,4M

Giải thích các bước giải:
a Để tính nồng độ % của dung dịch CuSO4 bão hòa ở nhiệt độ trên, ta dùng công thức:
Nồng độ % = (Khối lượng chất tan/Công thức phân tử chất tan) / Thể tích dung dịch x 100%
Với dung dịch CuSO4 bão hòa ở 60 độ C, ta có:
Khối lượng chất tan (CuSO4) = 40 kg = 40000 g
Thể tích dung dịch = 100 ml = 100 cm^3
Công thức phân tử CuSO4: 1 Cu + 1 S + 4 O = 63.5 + 32 + 4 x 16 = 159.5
Nồng độ % = (40000/159.5) / 100 = 25.08 %
Vậy, nồng độ % của dung dịch CuSO4 bão hòa ở nhiệt độ 60 độ C là khoảng 25.08 %.
b) Để tính khối lượng H2O cần dùng để pha vào dung dịch trên và có được dung dịch CuSO4 10%, ta dùng công thức:
Khối lượng H2O = Khối lượng chất tan ban đầu - Khối lượng chất tan sau pha / (Nồng độ sau pha - Nồng độ ban đầu)
Giả sử khối lượng chất tan sau khi pha là x g (= 10/100 x khối lượng dung dịch sau khi pha)
Vậy, ta có:
Khối lượng chất tan sau pha = 32 g + x g
Nồng độ sau pha = 10%
Nồng độ ban đầu = 25.08 %
Ứng dụng công thức, ta có:
x = (32 - 0.1 x (32 + x)) / (0.100 - 0.2508)
10000 x = 32 - 0.1 x (32 + x)
10000 x = 32 - 3.2 - 0.1x^2
0.1x^2 - 9967.2x + 3.2 = 0
Giải phương trình trên bằng phương pháp giải phương trình bậc hai ta có:
x ≈ 0.3145 hoặc x ≈ 9965.88
Với x ≈ 0.3145, ta được khối lượng H2O ≈ 32 - 0.3145 = 31.6855 g
Vậy, để có được dung dịch CuSO4 10%, ta cần dùng khoảng 31.6855 g nước.
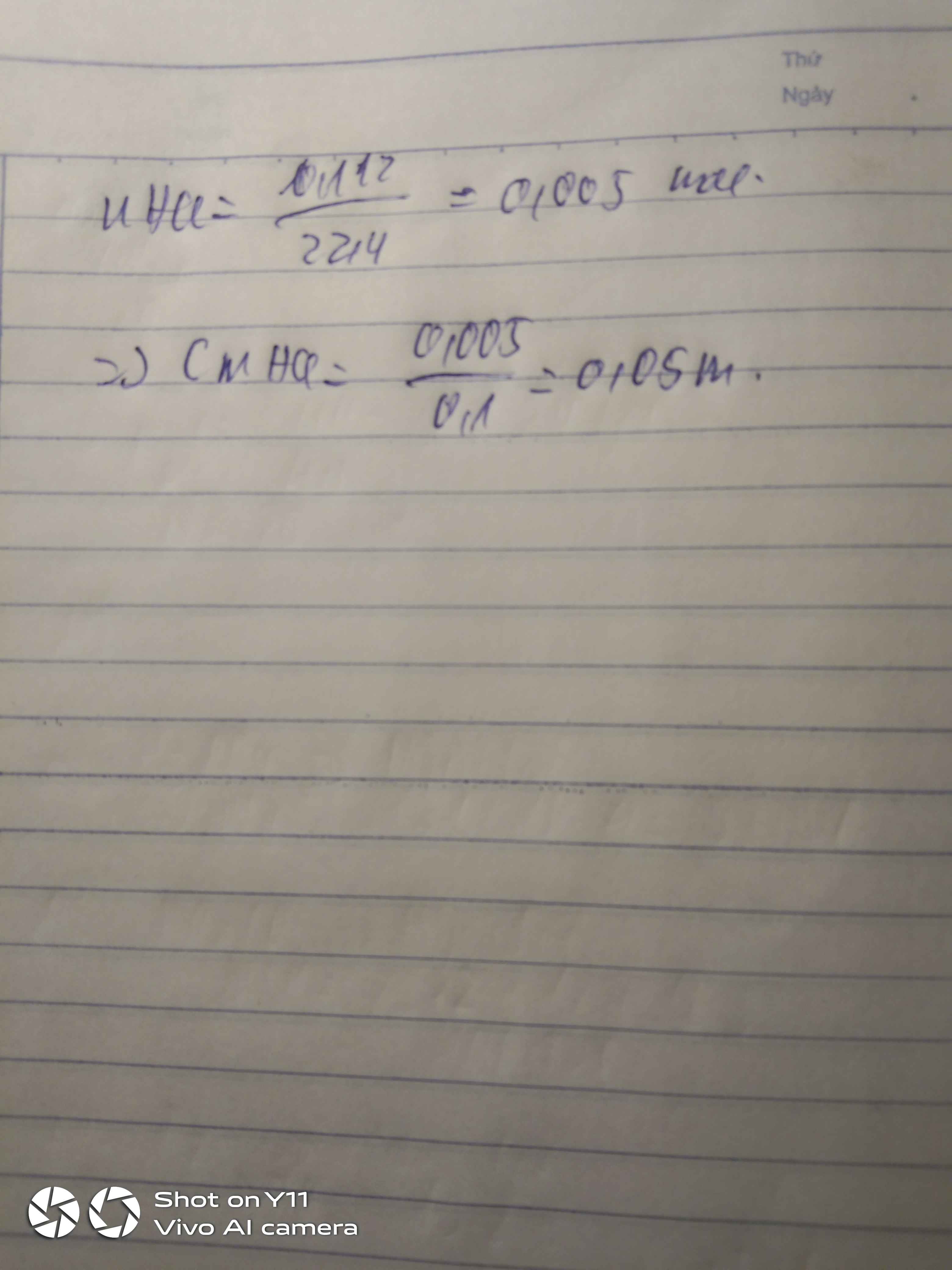
Câu 2:
\(m_{KCl}=\frac{200\times34}{100}=68\left(g\right)\)
Câu 3:
\(m_{ddH_2SO_4}=\frac{380}{95\%}=400\left(g\right)\)
\(\Rightarrow m_{H_2SO_4}=400\times5\%=20\left(g\right)\)
Câu 4:
\(n_{NaOH}=1,5\times1,5=2,25\left(mol\right)\)
\(V_{ddNaOH.1M}=\frac{2,25}{1}=2,25\left(l\right)\)
\(V_{H_2O}thêm=2,25-1,5=0,75\left(l\right)\)