Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chuyển các số và phân số về phân số dạng tối giản:
So sánh các số hữu tỉ dương:
Tương tự so sánh các số hữu tỉ âm với nhau.
Kết luận:
II. Trắc Nghiệm
Câu 1: Cho x = | x| kết quả nào đúng sau đây
a. x = 0
b. x = 1
c. x > 0
d. x ≥ 0
Câu 2: Trong các phân số sau, phân số nào biểu diễn số hữu tỷ 2/-5?
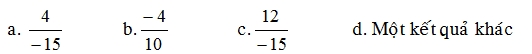
=> Chọn B
Câu 3: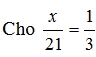 
giá trị của x bằng bao nhiêu?
a. 63
b. 1/7
c. 7
d. 0,7
Câu 4: 76 + 75 – 74 chia hết cho:
a. 5
b.7
c.11
d. Cả 3 số trên
Câu 5: Kết quả nào sau đây là đúng ?
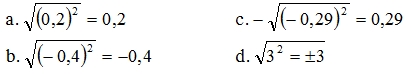
=> Chọn A
Câu 6: Câu nào trong các câu sau đây SAI
ĐỀ 2
I. PHẦN TRẮC NGHIỆM: (3 điểm)
Khoanh tròn chữ cái đứng trước câu trả lời đúng:
1. Trong các khẳng định sau, khẳng định sai là:
A. I ⊂ R
B. I ∪ Q = R
C. Q ⊂ I
D. Q ⊂ R
2. Kết quả của phép nhân (-0,5)3.(-0,5) bằng:
A. (-0,5)3
B. (-0,5)
C. (-0,5)2
D. (0,5)4
3. Giá trị của (-2/3) ³ bằng:
=> Chọn B
4. Nếu | x | = |-9 |thì:
A. x = 9 hoặc x = -9
B. x = 9
B. x = -9
D. Không có giá trị nào của x để thỏa mãn
5. Kết quả của phép tính 36.34. 32 bằng:
A. 2712
B. 312
C. 348
D. 2748
=> 39168
6. Kết quả của phép tính 
a) 4/3 x 2/5 - 3/4 x 2/5
= (4/3 - 3/4) x 2/5
= 7/12 x 2/5
= 7/30
b) 3 x ( -4/30)2 - 7/3
= 3 x 4/225 - 7/3
= 4/75 - 7/3
= -2,28
c) -0,8 x 1/9/25 - 4/5 x 64/25
= -4/5 x 1,36 - 4/5 x 2,56
= -4/5 x (1,36 - 2,56)
= -4/5 x (-1,2)
= 0,96
I. TRẮC NGHIỆM KHÁCH QUAN (3đ)
Khoanh tròn vào đáp án đúng trong các câu sau:
Câu 1: Trong các câu sau, câu nào sai
A. Nếu a là số thực thì a là số hữu tỉ hoặc số vô tỉ
B. Nếu b là số vô tỉ thì b viết được dưới dạng số thập phân vô hạn không tuần hoàn
C. Nếu c là số vô tỉ thì c cũng là số thực
D. Nếu c là số thực thì c cũng là số vô tỉ
Câu 2: Kết qủa của phép tính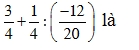 
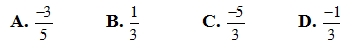
=> Chọn B
Câu 3: Kết qủa của phép tính 36 . 32 =
A. 98
B. 912
C. 38
D. 312
=> 1152
Câu 4: Từ đẳng thức a.d = b.c có thể suy ra tỉ lệ thức nào sau đây:
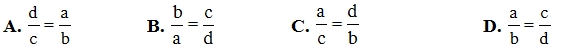
=> Chọn D
Câu 5: Viết số thập phân hữu hạn dưới dạng phân số tối giản :
=> Chọn A
Câu 6: Nếu √x = 3 thì x =
A. 3
B. 9
C. -9
D. ±9
II. TRẮC NGHIỆM TỰ LUẬN (7đ)
Bài 1 (1,5đ) Tính:
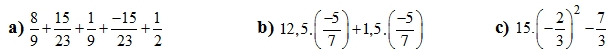
\(=\left(\frac{8}{9}+\frac{1}{9}\right)+\left(\frac{15}{23}-\frac{15}{13}\right)+\frac{1}{2}\) \(=\left(-\frac{5}{7}\right)\times\left(12,5+1,5\right)\) \(=15\times\frac{4}{9}-\frac{7}{3}\)
\(=\frac{9}{9}+0+0,5\) \(=\left(-\frac{5}{7}\right)\times14\) \(=\frac{20}{3}-\frac{7}{3}\)
\(=1+0,5\) \(=-10\) \(=\frac{13}{3}\)
\(=1,5\)
Bài 2 (2đ): Ba lớp 8A, 8B, 8C trồng được 180 cây . Tính số cây trồng được của mỗi lớp, biết rằng số cây trồng được của mỗi lớp lần lượt tỉ lệ với 4 : 6 : 8
Gọi số cây trồng được của lớp 8A, 8B, 8C theo thứ tự là a, b và c.
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{4}=\frac{b}{6}=\frac{c}{8}=\frac{a+b+c}{4+6+8}=\frac{180}{18}=10\)
\(\left[\begin{array}{nghiempt}\frac{a}{4}=10\\\frac{b}{6}=10\\\frac{c}{8}=10\end{array}\right.\)
\(\left[\begin{array}{nghiempt}a=10\times4\\b=10\times6\\c=10\times8\end{array}\right.\)
\(\left[\begin{array}{nghiempt}a=40\\b=60\\c=80\end{array}\right.\)
Vậy số cây trồng được của lớp 8A, 8B, 8C theo thứ tự là 40 cây, 60 cây và 80 cây.
Bài 3 (1,5đ): Tìm x, biết
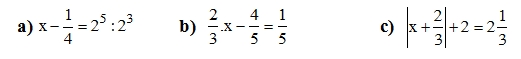
\(x-\frac{1}{4}=2^2\) \(\frac{2}{3}x=\frac{1}{5}+\frac{4}{5}\) \(\left|x+\frac{2}{3}\right|+\frac{6}{3}=\frac{7}{3}\)
\(x-\frac{1}{4}=4\) \(\frac{2}{3}x=\frac{5}{5}\) \(\left|x+\frac{2}{3}\right|=\frac{9}{3}-\frac{7}{3}\)
\(x=\frac{16}{4}+\frac{1}{4}\) \(x=1\div\frac{2}{3}\) \(\left|x+\frac{2}{3}\right|=\frac{2}{3}\)
\(x=\frac{17}{4}\) \(x=1\times\frac{3}{2}\) \(x+\frac{2}{3}=\pm\frac{2}{3}\)
\(x=\frac{3}{2}\) \(\left[\begin{array}{nghiempt}x+\frac{2}{3}=\frac{2}{3}\\x+\frac{2}{3}=-\frac{2}{3}\end{array}\right.\)
\(\left[\begin{array}{nghiempt}x=\frac{2}{3}-\frac{2}{3}\\x=-\frac{2}{3}-\frac{2}{3}\end{array}\right.\)
\(\left[\begin{array}{nghiempt}x=0\\x=-\frac{4}{3}\end{array}\right.\)
Bài 4 (1đ): So sánh các số sau: 2550 và 2300
2550 > 2300
Bài 5 (1đ): Cho N = 9/ (√x -5). Tìm x ∈ Z để N có giá trị nguyên.
\(N\in Z\)
\(\Leftrightarrow9⋮\sqrt{x}-5\)
\(\Leftrightarrow\sqrt{x}-5\in\text{Ư}\left(9\right)=\left\{-9;-3;-1;1;3;9\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{-4;2;4;6;8;14\right\}\)
\(\Leftrightarrow x\in\left\{\sqrt{-4};\sqrt{2};\sqrt{4};\sqrt{6};\sqrt{8};\sqrt{14}\right\}\)
mà \(x\in Z\)
=> x = 2
AB \(\perp\) AC (gt)
Có E nằm giữa A và C
=> AE<AC
=> BE<BC ( qh giữa đg xiên và hình chiếu ) (1)
Có D nằm giữa A và B
=> AD<AB
=> DE<BE ( qh giữa đg xiên và hc ) (2)
Từ (1) và (2) => DE<BC
a) \(\widehat{BEC}\) là góc ngoài của tam giác vuông ABE nên \(\widehat{BEC}\) là góc tù.
Do đó, tam giác BEC có BE < BC (BE là cạnh đối diện với góc tù) (1)
b) Ta có: AD, AB lần lượt là hình chiếu của ED, EB lên đường thẳng AB. Vì AD < AB => ED < EB (2)
Từ (1) và (2) ta có: DE < BC
Theo đề, ta có:
\(\dfrac{a+b-c}{3c}=\dfrac{b+c-a}{3a}=\dfrac{c+a-b}{3b}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{a+b-c}{3c}=\dfrac{b+c-a}{3a}=\dfrac{c+a-b}{3b}=\dfrac{a+b-c+b+c-a+c+a-b}{3c+3a+3b}=\dfrac{a+b+c}{3c+3a+3b}\)
\(=\dfrac{a+b+c}{3.\left(a+b+c\right)}=\dfrac{1}{3}\)
\(\Rightarrow\dfrac{a+b-c}{3c}=\dfrac{1}{3}\Rightarrow a+b-c=\dfrac{3c}{3}=c\Rightarrow a+b=2c\)
và \(\dfrac{b+c-a}{3a}=\dfrac{1}{3}\Rightarrow b+c-a=\dfrac{3a}{3}=a\Rightarrow b+c=2a\)
và \(\dfrac{c+a-b}{3b}=\dfrac{1}{3}\Rightarrow c+a-b=\dfrac{3b}{3}=b\Rightarrow c+a=2b\)
\(\Rightarrow P=\left(1+\dfrac{b}{a}\right)\left(1+\dfrac{a}{c}\right)\left(1+\dfrac{c}{b}\right)=\left(\dfrac{a+b}{a}\right)\left(\dfrac{c+a}{c}\right)\left(\dfrac{b+c}{b}\right)\)
\(=\left(\dfrac{2c}{a}\right)\left(\dfrac{2b}{c}\right)\left(\dfrac{2c}{b}\right)=\dfrac{2c.2a.2b}{a.b.c}=8\)
Vậy P = 8
ĐỀ 1
A/ PHẦN TRẮC NGHIỆM (3 điểm)
Khoanh tròn chữ cái đầu câu trả lời đúng nhất:
Câu 1: Tính 53. 52 =
A: 55
B: 56
C: 255
D: 256
=> 2756
Câu 2: Tính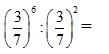 
=> Chọn A
Câu 3: Điền số thích hợp vào ô trống [(- 0,2 )6 ]5 = (-0,2) ….
A/ 11
B/ 30
C/ 56
D/ 65
Câu 4: Kết quả nào sai?
=> Chọn D
Câu 5: |x | = 11 thì x bằng:
A/ 11
B/ – 11
C/ ± 11
D/ Cả A, B, C đều sai.
Câu 6: √t = 4 thì t bằng:
A/ 16
B/ ±16
C/ 8
D/ ±8
a.
\(\frac{4^2\times4^3}{2^{10}}=\frac{4^2\times4^3}{2^{2\times5}}=\frac{4^2\times4^3}{\left(2^2\right)^5}=\frac{4^5}{4^5}=1\)
b.
\(\frac{\left(0,6\right)^5}{\left(0,2\right)^6}=\frac{\left(0,2\times3\right)^5}{\left(0,2\right)^6}=\frac{\left(0,2\right)^5\times3^5}{\left(0,2\right)^6}=\frac{243}{0,2}=1215\)
c.
\(\frac{2^7\times9^3}{6^5\times8^2}=\frac{2^7\times\left(3^2\right)^3}{\left(2\times3\right)^5\times\left(2^3\right)^2}=\frac{2^7\times3^6}{2^5\times3^5\times2^6}=\frac{3}{2^4}=\frac{3}{16}\)
d.
\(\frac{6^3+3\times6^2+3^3}{-13}=\frac{\left(2\times3\right)^3+3\times\left(3\times2\right)^2+3^3}{-13}=\frac{2^3\times3^3+3\times3^2\times2^2+3^3}{-13}=\frac{8\times3^3+3^3\times4+3^3}{-13}\)\(=\frac{3^3\times\left(8+4+1\right)}{-13}=\frac{27\times13}{-13}=-27\)
a/ \(\frac{4^2.4^3}{2^{10}}=\frac{4^5}{2^{10}}=\frac{\left(2^5\right)^2}{2^{10}}=\frac{2^{10}}{2^{10}}=1\)
b/\(\frac{\left(0,6\right)^5}{\left(0,2\right)^6}=\frac{\left(0,6\right)^5}{\left(0,2\right)^5.\left(0,2\right)}=\left(\frac{0,6}{0,2}\right)^5.\frac{1}{\frac{1}{5}}=3^5.5=243.5=1215\)
c/ \(\frac{2^7.9^3}{6^5.8^2}=\frac{2^7.\left(3^2\right)^3}{\left(2.3\right)^5.\left(2^3\right)^2}=\frac{2^7.3^6}{2^5.3^5.2^6}=\frac{2^7.3.3^5}{2^7.2^4.3^5}=\frac{3}{16}\)
d/ \(\frac{6^3+3.6^2+3^3}{-13}=\frac{\left(2.3\right)^3+3.\left(2.3\right)^2+3^3}{-13}=\frac{2^3.3^3+3.2^2.3^2+3^3}{-13}=\frac{3^3.\left(2^3+2^2+1\right)}{-13}=\frac{27.13}{-13}=-27\)
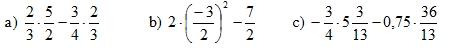
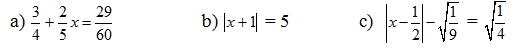
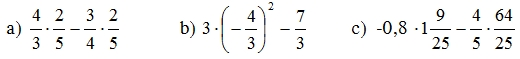
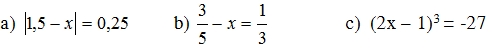
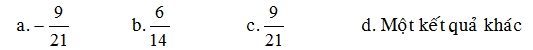
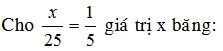
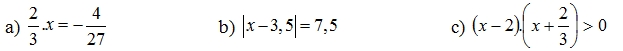
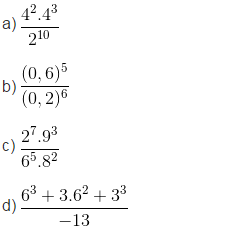
\(A=\left(6-\frac{2}{3}+\frac{1}{2}\right)-\left(5+\frac{5}{3}-\frac{3}{2}\right)-\left(3-\frac{7}{3}+\frac{5}{3}\right)\)
\(=>6-\frac{2}{3}+\frac{1}{2}-5-\frac{5}{3}+\frac{3}{2}-3+\frac{7}{3}-\frac{5}{3}\)
\(=>\left(\frac{2}{3}-\frac{5}{3}-\frac{5}{3}\right)+\left(\frac{1}{2}+\frac{3}{2}+\frac{7}{3}\right)+\left(6-5-3\right)\)
\(=>-242+353+\left(-2\right)\)
\(=>109\)