Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x là số thóc kho thứ nhất
y là số thóc kho thứ hai
Vì hai kho thóc có 250 tấn gạo.
Nên ta có phương trình: x + y = 250
Vì chuyển từ kho thứ nhất sang kho thứ hai 15 tấn thì số gạo kho thứ hai bằng 2/3 số gạo kho thứ nhất.
Nên ta có phương trình: y+15=2/3(x-15)
=> y - 2/3x= -15-10
=>y - 2/3x= -25
Ta có hệ phương trình: \(\hept{\begin{cases}x+y=250\\\frac{-2}{3}x+y=-25\end{cases}}\)
<=>\(\hept{\begin{cases}x=165\\y=85\end{cases}}\)
Vậy kho 1 có 165 tấn thóc, kho 2 có 85 tấn thóc.

Gọi số thóc của kho thứ nhất là x(tấn)(Điều kiện:0<x<100)
Số thóc của kho thứ hai là: 100-x(tấn)
Theo đề, ta có phương trình:
x-10=100-x+10
\(\Leftrightarrow x-10=110-x\)
\(\Leftrightarrow x+x=110+10\)
\(\Leftrightarrow2x=120\)
hay x=60(thỏa ĐK)
Vậy: Số thóc ban đầu của kho thứ nhất là 60 tấn
Số thóc ban đầu của kho thứ hai là 40 tấn
Gọi số thóc ở kho 1 là x, ở kho 2 là y (x>10,y>0)
Ta có tổng 2 kho là 100 tấn nên: x+y=100 (1)
Nếu chuyển kho thứ nhất sang kho thứ 2 10 tấn thí số thóc 2 kho bằng nhau nên: x-10=y+10 => x-y=20 (2)
Từ (1)(2) ta cộng vế với vế => 2x=120 <=> x=60 (tm)
Nên kho thứ nhất có 60 tấn, kho thứ 2 có 100-60=40 tấn

Vì khi chuyển số gạo từ bao này sang bao kia thì tổng số gạo cũng không thay đổi .
Ta có sơ đồ sau khi chuyển 50 tấn từ kho thứ 1 sang kho thứ 2 :
Kho thứ 1 : |----|----|----|----|----| tổng số gạo ở 2 kho là 450 tấn
Kho thứ 2 : |----|----|----|----|
Số hàng ở kho thứ nhất sau khi chuyển là : 450:(5+4)*5=225(tấn)
Số hàng ở kho thứ nhất lúc đầu là : 225-50=175 (tấn)
Số hàng ở kho thứ 2 lúc đầu là : 450-175=275 (tấn)
Đáp số : kho thứ nhất : 175 tấn
kho thứ hai : 275 tấn

Lời giải:
Gọi số thóc ban đầu ở kho 1 và kho 2 lần lượt là $a$ và $a+200$ (tấn)
Theo bài ra ta có:
$a+200-400=(a+400).\frac{5}{8}$
$\Leftrightarrow a-200=\frac{5}{8}(a+400)$
$\Leftrightarrow a=1200$ (tấn)
Vậy kho 1 có $1200$ tấn thóc, kho 2 có $1200+200=1400$ tấn thóc.

Gọi khối lượng thóc ở kho 1 ban đầu là x
Khối lượng thóc ban đầu ở kho 2 là x+200
Theo đề, ta có:
x-200=5/8(x+400)
=>x-200=5/8x+250
=>3/8x=450
hay x=1200
Vậy: Kho 1 có 1200 tấn, kho 2 có 1400 tấn

a) Theo đề bài, mỗi ngày xuất đi m (tấn) với 0 < m < 60.
=> x ngày xuất đi m.x (tấn).
Vậy khối lượng xi măng còn lại trong kho sau x ngày xuất hàng là:
60 - mx (tấn)
Mà y (tấn) là khối lượng xi măng còn lại trong kho sau x ngày xuất hàng.
=> y = 60 - mx hay y = -mx + 60 (m \( \ne \) 0)
Vậy y là hàm số bậc nhất của biến x (đpcm).
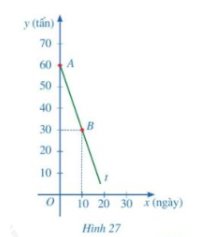
b) Từ hình 27, tia At đi qua hai điểm A(0; 60); B(10; 30)
Thay tọa độ điểm A(0; 60) vào hàm số bậc nhất y = ax + b \(\left( {a \ne 0} \right)\)ta được:
60 = a. 0 + b suy ra b = 60
Hàm số bậc nhất là y = ax + 60 (1)
Thay tọa độ B(10; 30) vào hàm số bậc nhất (1) ta có:
30 = a. 10 + 60 suy ra a = -3
Vậy y = -3x + 60
Với x = 15 ta có y = -3.15 + 60 = 15
Vậy trong kho còn lại 15 tấn xi măng sau 15 ngày.

gọi a là số hàng ở kho 2 (đk a,b>50,nguyên).
b là số hàng ở kho 1
ta có: a+b=450 (1)
5/4 (a-50)=b+50
=> 5/4a-b = 112,5 (2)
từ (1) và (2) ta có hệ phương trình :
a+b=450 <=> 5/4xa +5/4xb =562,5 => 9/4xb=450
5/4a-b = 112,5 5/4a-b = 112,5 a+b=450
=>a=200,b=250 (chọn)
vậy kho 1 có 250 tấn hàng
kho 2 có 200 tấn hàng.
Gọi số xi măng ở kho thứ nhất ban đầu là : x ( tấn ; x > 0)
số xi măng ở kho thứ hai ban đầu là : x - 50 ( tấn)
Số xi măng còn lại ở kho thứ nhất là ; x - 20 ( tấn)
Số xi măng nhận thêm ở kho thứ hai là : x - 30 ( tấn )
Do sau khi thay đổi thì số xi măng kho thứ nhất bằng \(\dfrac{4}{3}\) kho thứ hai , ta có PT sau :
x - 20 = \(\dfrac{4}{3}\)( x - 30)
⇔ x - 20 = \(\dfrac{4x}{3}\) - 40
⇔\(\dfrac{4x}{3}\) - x = 20
⇔ \(\dfrac{x}{3}\) = 20
⇔ x = 60 ( tấn )
Vậy kho thứu hai ban đầu là : x - 50 = 10 ( tấn )