Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

![]()
- LUYỆN TẬP
- HỎI ĐÁP
- KIỂM TRA
⋯
TRỢ GIÚP
- 1
 khoilaba
khoilaba
Giúp tôi giải toán và làm văn
Tìm kiếm
- Mới nhất
- Chưa trả lời
- Câu hỏi hay
- Câu hỏi tôi quan tâm
- Câu hỏi của bạn bè
- Gửi câu hỏi
Tất cảToánTiếng ViệtTiếng Anh

KHANH QUYNH MAI PHAM
Trả lời
0
Đánh dấu
Hôm kia lúc 10:03
Cho phương trình
x2−2mx+2m−1=0
Tìm m để phương trình đã cho có 2 nghiệm phân biệt x1, x2 thỏa mãn lx1-x2l=16
Toán lớp 9
![]()

Tiểu Duy Hồ Bạch
Trả lời
0
Đánh dấu
31 tháng 3 2019 lúc 9:56
cho tam giác nhọn ABC. Đường tròn tâm O đường kính BC cắt các cạnh AB,AC lần lượt tại các điểm M,N . Gọi H là gia điểm BN, CM; P là giao điểm AH và BC
1. Chứng minh tứ giác AMHN nội tiếp đường tròn
2. Chứng minh BM.BA=BP.BC
3. Trong trường hợp đặc biệt khi tam giác ABC đều cạnh bằng 2a. Tính chu vi đường tròn ngoại tiếp tứ giác AMHN theo a
4. Từ A kẻ các tiếp tuyển AE và AF của đường tròn tâm O đường kính BC ( E,F là các tiếp điểm). Chứng minh ba điểm E,H,F thằng hàng
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn C tâm O bán kính R. Hai đường cao AE và BK của tam giác ABC cắt nhau tại H ( với E thuộc BC, K thuộc AC)
1. Chứng minh tg AEBK nội tiếp đường tròn
2. Chứng minh CE.CB=CK.CA
3. Chứng minh góc OCA = góc BAE
Đọc tiếp...
Được cập nhật Hôm kia lúc 12:35
Câu hỏi tương tự Đọc thêm Báo cáo
Toán lớp 8
![]()

Nguyen Thi Phung
Trả lời
0
Đánh dấu
26 tháng 5 2018 lúc 14:58
Cho nửa đường tròn đường kính AB và 1 điểm M bất kì trên nửa đường tròn đó ( M khác A , B ) . Trên nửa mặt phẳng bờ AB chứa nửa đường tròn người ta vẽ tiếp tuyến Ax . Tia BM cắt tia Ax tại I ; tia phân giác của ^IAMcắt nửa đường tròn tại E , cắt tia BM tại F . Tia BE cắt Ax tại H , cắt AM tại K .
a) Chứng minh rằng :
IA2=IM.IB
b) Chứng minh : Tam giác BAF cân .
c) Chứng minh : tứ giác AKFH là hình thoi
d) Xác định vị trí M để tứ giác AKFI nội tiếp được đường tròn .
Đọc tiếp...
Được cập nhật Hôm kia lúc 12:22
Toán lớp 9
![]()

Khanhthien Lê
Trả lời
0
Đánh dấu
31 tháng 3 lúc 8:44
Cho đường tròn (O;R) và một điểm A sao cho OA = R . Vẽ các tiếp tuyến AB, AC với đường tròn (A, B là các tiếp điểm). Vẽ góc xOy bằng 450 cắt đoạn thẳng AB và AC lần lượt tại D và E. Chứng minh rằng:
Được cập nhật Hôm kia lúc 11:45
Toán lớp 9
![]()

Nguyễn Phương Thảo
Trả lời
0
Đánh dấu
Hôm kia lúc 11:41
BÀI 1:
Trả lời câu 3 (trang 43 sgk Ngữ Văn 6 Tập 2):
Dựa vào bài Vượt thác, hãy viết một đoạn văn từ ba đến năm câu tả dượng
Hương Thư đưa thuyền vượt qua thác dữ; trong đoạn văn có sử dụng cả hai
kiểu so sánh đã được giới thiệu.
GỢI Ý: Hướng dẫn viết đoạn văn:
- Hình thức: Từ 3- 5 câu diễn đạt mạch lạc.
- Nội dung: tả cảnh dượng Hương Thư đưa thuyền vượt qua thác dữ.
- Kĩ năng: Sử dụng hai kiểu so sánh ngang bằng và so sánh không ngang bằng.
Đoạn văn tham khảo 1
Nước từ trên cao phóng xuống định nuốt chửng con thuyền. Nhưng ở phía dưới
dượng Hương Thư nhanh như cắt vừa thả sào, vừa rút sào nhịp nhàng, đều đặn.
Con thuyền được giữ thăng bằng xé ngang dòng nước lao nhanh. Nó chồm lên, sấn
tới, hùng dũng hơn cả dòng thác dữ.
Đoạn văn tham khảo 2: Cảnh Dượng Hương Thư vượt thác được coi là một
trong những đoạn đặc sắc nhất mà tác giả Võ Quảng viết về hành trình người lao
động chinh phục khó khăn, thử thách. Nước từ trên cao đổ xuống hung hãn như
muốn nuốt con thuyền. Dượng Hương Thư bình tĩnh ghì chặt đầu sào, chuyển
hướng thuyền lao nhanh về phía trước. Nhìn dượng lúc đó oai hùng hơn một dũng
sĩ rừng xanh.
ĐOẠN VĂN CỦA HS:
BÀI 2: Chỉ ra và phân tích hiệu quả của biện pháp tu từ so sánh trong đoạn thơ sau:
Những ngôi sao thức ngoài kia
Chẳng bằng mẹ đã thức vì chúng con
Đêm nay con ngủ giấc tròn
Mẹ là ngọn gió của con suốt đời
( Trần Quốc Minh- Mẹ)
GỢI Ý:
+ Nhớ lại các bước làm 1 bài tập tu từ ( 3 bước)
- Gọi tên BPTT
Đọc tiếp...
Ngữ Văn lớp 6
![]()

Nguyễn Tiến Quang Vinh
Trả lời
0
Đánh dấu
Hôm kia lúc 9:47
Tìm số tự nhiên m và n sao cho 6^m+2^n+2 là số chính phương
Toán lớp 8
![]()

Nguyễn Thanh Hà
Trả lời
0
Đánh dấu
31 tháng 3 lúc 8:12
Cho hệ phương trình : {
| (m−1)x−my=3m−1 |
| 2x−y=m+5 |
a) Gỉai và biện luận hệ phương trình theo m
b) Với giá trị nguyên nào của m để hai đường thẳng của hệ cắt nhau tại 1 điểm nằm trong góc phần tư thứ IV của hệ tọa độ Oxy
GIÚP MÌNH VỚI Ạ !THANKS NHIỀU !!
Đọc tiếp...
Được cập nhật Hôm kia lúc 11:35
Toán lớp 9
![]()

Nguyễn Trần Lâm
Trả lời
0
Đánh dấu
30 tháng 3 lúc 14:06
Cho biểu thức 4x^{2}+3x+44x2+3x+4.
Giá trị biểu thức
1) tại x = 3x=3 là
.
2) tại x = 0x=0 là
.
3) tại x = -3x=−3 là
.
Đọc tiếp...
Được cập nhật 30 tháng 3 lúc 18:29
Toán lớp 7
![]()

Hoàng Bin
Trả lời
0
Đánh dấu
Hôm kia lúc 12:09
1.Thực hiện phép chia
a,(163-642):82
b,(5x4-3x3+x2):3x2
c,(5xy2+9xy-x2y2):(-xy)
2.Tìm số tự nhiên n để mỗi phép chia sau là phép chia hết
a,(5x3-7x2+x5):3xn
b,(13x4y3-5x3y3+6x2y):5xnyn
3.Tìm a,b để đa thức 2x3+ax+b chia cho x+1 dư -6 và chia cho x-2 dư 21 (Dùng định lý Bơ Du)
Bạn nào biết thì làm nhanh giùm mình với nhé !
Đọc tiếp...
Toán lớp
![]()

juni
Trả lời
0
Đánh dấu
Hôm kia lúc 12:50
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (C) tâm O bán kính R. Hai đường cao AE và BK của tam giác ABC cắt nhau tại H ( với E thuộc BC, K thuộc AC).
1. Chứng minh tứ giác ABEK nội tiếp được trong một đường tròn
2. Chứng minh CE.CB = CK.CA
3.Chứng minh góc OCA = góc BAE
4. Cho B,C cố định và A di động trên (C) nhưng vẫn thoả mãn điều kiện tam giác ABC nhọn; khi đó H thuộc 1 đường tròn (T) cố định. Xác định tâm I và tính bán kính r của đường tròn (T), biết R=3cm.
Đọc tiếp...
Toán lớp
![]()

tramy
Trả lời
0
Đánh dấu
Hôm kia lúc 12:58
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (C) tâm O bán kính R. Hai đường cao AE và BK của tam giác ABC cắt nhau tại H ( với E thuộc BC, K thuộc AC.
1. Chứng minh tứ giác ABEK nội tiếp được đường tròn.
2. Chứng minh CE.CB=CK.CA
3. Chứng minh góc OCA = góc BAE
4. Cho B,C cố định và A di động trên (C) nhưng vẫn thỏa mãn điều kiện tam giác ABC nhọn; khi đó H thuộc 1 đường tròn (T) cố định. Xác định tâm I và tính bán kính r của đường tròn (T), biết R= 3cm
giúp mình với ạ, mình cần gấp
Đọc tiếp...
Toán lớp
![]()

Hoàng Lâm Tùng tew
Trả lời
0
Đánh dấu
Hôm kia lúc 16:41
Từ điểm M nằm ngoài đường tròn (O;R), vẽ tiếp tuyến MA và cát tuyến MBC ( B nằm giữa M và C )
a) CM: MA.MA=MB.MC
b) Gọi BD, CE lần lượt là hai đường cao của tam giác ABC. CM: ED song song MA
c) Tia DE cắt MC tại F.FA cắt đường tròn (O) tại G. CM: GEA=GFB
Đọc tiếp...
Toán lớp
![]()

Chống Đạn
Trả lời
0
Đánh dấu
Hôm kia lúc 16:42
Tìm cụm danh từ trong đoạn văn sau đây vẽ lại cụm danh từ vừa tìm được Điền vào chỗ trống cụm danh từ vừa tìm được hoàn thành
Ngày xưa có một ông vua sai một viên quan đi dò la khắp nước tìm người tài giỏi. Viên quan ấy đã đi nhiều nơi, đến đâu cũng đưa ra những câu đố oái oăm để hút mọi người, nhưng tuy mất nhiều công mà chưa thấy có người nào thật lỗi lạc.
Một hôm, viên quan đi qua một cánh đồng làng kia, chợt thấy bên vệ đường có hai cha con nhà nọ đang làm ruộng: cha đánh trâu cày, con đập đất. Ông bèn dừng ngựa lại hỏi:
Đọc tiếp...
Toán lớp
![]()

Hồ Thị Ngọc Như
Trả lời
0
Đánh dấu
Hôm kia lúc 16:43
Có tồn tại hay không số:
22...22 chia hết cho 23(n số 2 )
Toán lớp
![]()

Tiến Đạt
Trả lời
0
Đánh dấu
Hôm kia lúc 16:36
(3√aa+√a+b −3aa√a−b√b +1√a−√b ):(a−1)(√a−√b)(2a+2√ab+2b)
a. Rút gọn P
b. Tìm giá trị nguyên của a để giá trị P nguyên
Toán lớp 9
![]()

Bùi Thị Thương
Trả lời
0
Đánh dấu
Hôm kia lúc 15:56
Bạn Hà gửi bưu thiết và thư cho 15 người bạn của mình tổng số tiền phải trả là là 4680₫ nếu tiền tem 200₫ cho mỗi bưu thiếp là 320₫ đồng cho mỗi lá thư như thì bạn Hà phải trả bao nhiêu tiền bưu thiếp?
Toán lớp 5
![]()

Lý Huyền Trang
Trả lời
0
Đánh dấu
Hôm kia lúc 15:01
CMR: A= 3n+3 - 22 .3n + 2n+5 - 33 . 2n chia hết cho 23
Toán lớp 7
![]()

Bangtan Bàngtán Bất Bìnhtĩnh
Trả lời
0
Đánh dấu
Hôm kia lúc 15:01
cho tam giác ABC, AC=9cm,BC=10cm,AB=6cm, đường phân giác trong AD, đường phân giác ngoài AE
a) tính DB,DC,BE
b)đường phân giác CF của tg ABC cắt AD ở I. tính tỉ số diện tích tg DIF và ABC
Toán lớp 8
![]()

Bùi Thanh Bình
Trả lời
0
Đánh dấu
Hôm kia lúc 15:07
Trên tia Gz lấy điểm H sao cho GH =17dm. Trên tia đối của Gz lấy điểm M sao cho GM
giúp miki với mik đang cần gấp mik k cho nha!
Toán lớp 6
![]()

Đạt
Trả lời
0
Đánh dấu
Hôm kia lúc 15:28
Giúp mình với, sắp nộp bài r.
Cho ∆ABC đồng dạng ∆DEF , biết AB = 5cm, DE = 9cm.
a. Viết tên các cặp góc bằng nhau
b. Tìm tỉ số đồng dạng
c. Tính P và P’. Với P và P’ lần lượt là chu vi của ∆ABC và ∆DEF, biết P’ + P = 28.
Đọc tiếp...
Toán lớp 8
![]()
Tải thêm câu hỏi
Nội quy chuyên mục
Giải thưởng hỏi đáp
Danh sách chủ đề
Toán lớp 1Toán lớp 2Toán lớp 3Toán lớp 4Toán lớp 5Toán lớp 6Toán lớp 7Toán lớp 8Toán lớp 9Toán lớp 10Toán lớp 11Toán lớp 12Tiếng Việt 1Tiếng Việt 2Tiếng Việt 3Tiếng Việt 4Tiếng Việt 5Ngữ Văn 6Ngữ Văn 7Ngữ Văn 8Ngữ văn 9Ngữ văn 10Ngữ văn 11Ngữ văn 12Tiếng Anh lớp 1Tiếng Anh lớp 2Tiếng Anh lớp 3Tiếng Anh lớp 4Tiếng Anh lớp 5Tiếng Anh lớp 6Tiếng Anh lớp 7Tiếng Anh lớp 8Tiếng Anh lớp 9Tiếng Anh lớp 10Tiếng Anh lớp 11Tiếng Anh lớp 12
Xếp hạng tuần
![]()
Lê Nhật Hằng
Điểm SP: 193. Điểm GP: 0.
![]()
『✰Ğấʉ ✰』
Điểm SP: 175. Điểm GP: 0.
![]()
Phượng Thiên Hoàng Y ( Team ~ Thiên ~ ❄️ Nguyệt ~🌙 )
Điểm SP: 164. Điểm GP: 0.
![]()
𝑮𝒊𝒂 𝑯𝒖𝒚
Điểm SP: 120. Điểm GP: 0.
![]()
Nhật Quỳnh
Điểm SP: 117. Điểm GP: 23.
![]()
゚° ღϮɦẩ๓ йǥųуệϮ Łyღ° ゚
Điểm SP: 113. Điểm GP: 1.
![]()
Nguyễn Lê Khánh Linh
Điểm SP: 101. Điểm GP: 0.
![]()
★๖ۣۜMĭηʑ☆๖ۣۜŇɦạϮッт๏áɴ๖ۣۜнọςッ
Điểm SP: 94. Điểm GP: 3.
![]()
๖ۣۜRan Mori๖ۣۜ.♡
Điểm SP: 91. Điểm GP: 0.
![]()
Trần Thu Hà
Điểm SP: 90. Điểm GP: 1.
Bảng xếp hạng
Có thể bạn quan tâm
ôn thi thpt môn toánôn thi thpt môn vật lýôn thi thpt môn hóa họcôn thi thpt môn sinh họcôn thi thpt môn tiếng anhôn thi thpt môn lịch sửôn thi thpt môn địa lýôn thi thpt môn giáo dục công dântài liệu tham khảo môn toántài liệu tham khảo môn ngữ văntài liệu tham khảo môn sinh họctài liệu tham khảo môn vật lýtài liệu tham khảo môn hóa họctài liệu tham khảo môn lịch sửtài liệu tham khảo môn địa lýtài liệu tham khảo môn tiếng anhtài liệu tham khảo môn giáo dục công dân
Tài trợ






Các câu hỏi không liên quan đến toán lớp 1 - 9 các bạn có thể gửi lên trang web h.vn để được giải đáp tốt hơn.
© 2013 - Trường Đại học Sư phạm Hà Nội (email: a@olm.vn)
103.35.64.88
![]()

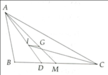
A B C H M O G N
Gọi M là trung điểm BC ; N là điểm đối xứng với H qua M.
M là trung điểm của BC và HN nên BNCH là hình bình hành
\(\Rightarrow NC//BH\)
Mà \(BH\perp AC\Rightarrow NC\perp AC\)hay AN là đường kính của đường tròn ( O )
Dễ thấy OM là đường trung bình \(\Delta AHN\) suy ra \(OM=\frac{1}{2}AH\)
M là trung điểm BC nên OM \(\perp\)BC
Xét \(\Delta AHG\)và \(\Delta OGM\)có :
\(\widehat{HAG}=\widehat{GMO}\); \(\frac{GM}{GA}=\frac{OM}{HA}=\frac{1}{2}\)
\(\Rightarrow\Delta AGH~\Delta MOG\left(c.g.c\right)\Rightarrow\widehat{AGH}=\widehat{MGO}\)hay H,G,O thẳng hàng
A B C D M N P Q E F T S
gọi E,F,T lần lượt là trung điểm của AB,CD,BD
Đường thẳng ME cắt NF tại S
Vì AC = BD \(\Rightarrow EQFP\)là hình thoi \(\Rightarrow EF\perp PQ\)( 1 )
Xét \(\Delta TPQ\)và \(\Delta SEF\)có : \(ME\perp AB,TP//AB\)
Tương tự , \(NF\perp CD;\)\(TQ//CD\)
\(\Rightarrow\Delta TPQ~\Delta SEF\)( Góc có cạnh tương ứng vuông góc )
\(\Rightarrow\frac{SE}{SF}=\frac{TP}{TQ}=\frac{AB}{CD}\)
Mặt khác : \(\Delta MAB~\Delta NCD\Rightarrow\frac{AB}{CD}=\frac{ME}{NF}\)( tỉ số đường cao = tỉ số đồng dạng )
Suy ra : \(\frac{ME}{NF}=\frac{SE}{SF}\)\(\Rightarrow EF//MN\)( 2 )
Từ ( 1 ) và ( 2 ) suy ra \(MN\perp PQ\)

A B C P Q I R D t
Ta có: \(\widehat{DQB}=\widehat{CQP}\)(2 góc đối đỉnh).
Dễ thấy CA và CB là hai tiếp tuyến của (I) \(\Rightarrow CP=CQ\)nên tam giác CPQ cân tại C
\(\Rightarrow\widehat{CQP}=\frac{180^0}{2}-\frac{\widehat{C}}{2}=90^0-\frac{\widehat{C}}{2}\Rightarrow\widehat{DQB}=90^0-\frac{\widehat{C}}{2}\left(1\right)\)
Lại có: \(\widehat{DIB}=\widehat{IAB}+\widehat{IBA}=\frac{1}{2}\widehat{A}+\frac{1}{2}\widehat{B}=\frac{1}{2}\left(180^0-\widehat{C}\right)=90^0-\frac{\widehat{C}}{2}\left(2\right)\)
Từ (1) và (2) suy ra: \(\widehat{DQB}=\widehat{DIB}\)=> Tứ giác BIQD nội tiếp đường tròn
=> \(\widehat{BDI}=\widehat{BQI}\). Mà \(\widehat{BQI}=90^0\)\(\Rightarrow\widehat{BDI}=90^0\)
Do đó \(AD\perp BD\)tại D hay \(AI\perp BD\)tại D
Ta thấy tam giác ABC vuông tại A có A; B cố định => \(\widehat{BAC}\)không đổi nên tia phân giác AI của \(\widehat{BAC}\)cố định
Do BD vuông góc với AI tại D (cmt) => BD cố định , vậy nên điểm D là điểm cố định.
Mà PQ đi qua D => PQ luôn đi qua 1 điểm D cố định khi C chuyển động trên tia At (đpcm).

Sorry vì hình vẽ ko chính xác.
Đường tròn (I) tiếp xúc với AB, AC tương ứng tại F và E. Gọi K là giao điểm của BI và DE, L là giao điểm của CI và DF.
I A B C D M N F E K L
Giả sử L nằm trong đoạn Df và K nằm trong đoạn DE. Các TH khác chứng minh tương tự.
Dễ thấy ^AIK = ^IAB + ^IBA = (^BAC + ^ABC)/2 = 90o - (^ACB)/2 = ^CED = 180o - ^AEK
^AIL = 180o - ^AFL. Chịu.
Giải tiếp:
Do đó các tứ giác AEKI, AFLI nội tiếp (1)
Vậy ^AKM =^AKI = ^AEI = 90o = ^AFI = ^ALI = ^ALN
Kết hợp AM vuông góc MN suy ra các tứ giác AKDM và ALDN nội tiếp(2)
Từ (1) và (2) suy ra ^DAM = ^DKM = 180 - ^EKI = ^EAI = ^CAI = ^BAI = ^FAI = 180 - ^FLI = ^DLI = ^DLN = ^DAM.
Từ đó với chúc ý AM \(\perp\) MN suy ra tam giác AMN cân tại A.

a,Chứng minh tam giác MPE đồng dạng với tam giác KPQ.
+PK là phân giác góc QPO.
=>^MPE = ^KPQ.(α) .
+ Tam giác OMN đều .=>^EMP=120 độ.
+ QK cũng là phân giác ^OQP.
=>^QKP = 180 - (^KQP+^KPQ).
Mà 2^KQP + 2^KPQ =180- 60 =120 độ.
=>^QKP=120 độ. Do đó:^EMP = ^QKP. (ß) .
Từ (α) và (ß), ta có tam giác MPE đồng dạng với tam giác KPQ.
b, Chứng minh tứ giác PQEF nội tiếp được trong đường tròn.
Do hai tam giác MPE và KPQ đồng dạng nên:^MEP=^KQP , hay: ^FEP=^FQP.
Suy ra, tứ giác PQEF nội tiếp được trong đường tròn.
c, Gọi D là trung điểm của đoạn PQ. Chứng minh tam giác DEF là một tam giác đều.
Do hai tam giác MPE và KPQ đồng dạng nên: PM/PK =PE/PQ . Suy ra: PM/PE =PK/PQ .
Ngoài ra: ^MPK=^EPQ . Do đó, hai tam giác MPK và EPQ đồng dạng.
Từ đó:^PEQ=^PMK=90độ .
Suy ra, D là tâm của đường tròn ngoại tiếp tứ giác PQEF.
Vì vậy, tam giác DEF cân tại D.
Ta có: ^FDP=2^FQD=^OQP ; ^EDQ=2^EPD=^OPQ .
^FDE=180 - (^FDP+^EDQ) =^POQ =60độ.
Từ đó, tam giác DEF là tam giác đều.