K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
10 tháng 10 2018
Hướng dẫn giải
Chọn C.
TH1: Nếu cosx =0 có sin2x = 1 không thỏa mãn phương trình.
TH2: 
chia cả hai vế của phương trình cho cos2x ta được:
PT
1
CM
7 tháng 9 2018
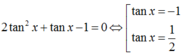
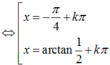
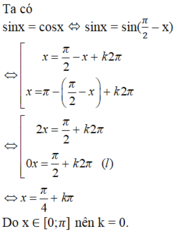
Vậy chỉ có 1 nghiệm của phương trình thuộc [0; .
Đáp án là A.
PT
1
CM
22 tháng 4 2017
Ta có sin x = cos x ⇔ sin x = sin π 2 − x
⇔ x = π 2 − x + k 2 π x = π − π 2 − x + k 2 π
⇔ x = π 4 + k π , k ∈ ℤ
Do x ∈ 0 ; π nên k = 0
Vậy phương trình chỉ có một nghiệm duy nhất
ĐÁP ÁN A
HP
13 tháng 8 2021
1.
a, Phương trình có nghiệm khi:
\(\left(m+2\right)^2+m^2\ge4\)
\(\Leftrightarrow m^2+4m+4+m^2\ge4\)
\(\Leftrightarrow2m^2+4m\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}m\ge0\\m\le-2\end{matrix}\right.\)
b, Phương trình có nghiệm khi:
\(m^2+\left(m-1\right)^2\ge\left(2m+1\right)^2\)
\(\Leftrightarrow2m^2+6m\le0\)
\(\Leftrightarrow-3\le m\le0\)
HP
13 tháng 8 2021
2.
a, Phương trình vô nghiệm khi:
\(\left(2m-1\right)^2+\left(m-1\right)^2< \left(m-3\right)^2\)
\(\Leftrightarrow4m^2-4m+1+m^2-2m+1< m^2-6m+9\)
\(\Leftrightarrow4m^2-7< 0\)
\(\Leftrightarrow-\dfrac{\sqrt{7}}{2}< m< \dfrac{\sqrt{7}}{2}\)
b, \(2sinx+cosx=m\left(sinx-2cosx+3\right)\)
\(\Leftrightarrow\left(m-2\right)sinx-\left(2m+1\right)cosx=-3m\)
Phương trình vô nghiệm khi:
\(\left(m-2\right)^2+\left(2m+1\right)^2< 9m^2\)
\(\Leftrightarrow m^2-4m+4+4m^2+4m+1< 9m^2\)
\(\Leftrightarrow m^2-1>0\)
\(\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\)
CM
31 tháng 10 2019
Đặt t = sin x + cos x − 2 ≤ t ≤ 2 ⇒ sin x cos x = t 2 − 1 2 .
Phương trình trở thành t 2 − 1 2 − t + m = 0 ⇔ − 2 m = t 2 − 2 t − 1 ⇔ t − 1 2 = − 2 m + 2 .
Do − 2 ≤ t ≤ 2 ⇒ − 2 − 1 ≤ t − 1 ≤ 2 − 1 ⇔ 0 ≤ t − 1 2 ≤ 3 + 2 2 .
Vậy để phương trình có nghiệm
⇔ 0 ≤ − 2 m + 2 ≤ 3 + 2 2 ⇔ − 1 + 2 2 2 ≤ m ≤ 1 → m ∈ ℤ m ∈ − 1 ; 0 ; 1 .
Chọn đáp án C.
Ta có:
\(\sqrt{3}sinx-cosx=0\\ \Leftrightarrow\dfrac{\sqrt{3}}{2}sinx-\dfrac{1}{2}cosx=0\)
Đặt \(\dfrac{\sqrt{3}}{2}=cos\dfrac{\Pi}{6};\dfrac{1}{2}=sin\dfrac{\Pi}{6}\)
\(\Rightarrow\dfrac{\sqrt{3}}{2}sinx-\dfrac{1}{2}cosx=0\Leftrightarrow cos\dfrac{\Pi}{6}sinx-sin\dfrac{\Pi}{6}cosx=0\\ \Leftrightarrow sin\left(x-\dfrac{\Pi}{6}\right)=0\\ \)
\(\Rightarrow x-\dfrac{\Pi}{6}=k\Pi,k\inℤ\\ \Rightarrow x=\dfrac{\Pi}{6}+k\Pi,k\inℤ\)