Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Ta có:
9 x + 9 − x = 2 ⇔ 3 x 2 + 1 3 x 2 = 23 ⇔ 3 x 2 + 2.3 x . 1 3 x + 1 3 x 2 = 25 ⇔ 3 x + 3 − x = 5.
Vậy A = 5 + 5 1 − 5 = 10 − 4 = − 5 2 = a b → a . b = − 5 .2 = − 10.

Đáp án A.
Phương trình đã cho tương đương với:
2 x 2 + m x + 1 = x 2 + 6 x + 9 x ≥ − 3 ⇔ x 2 + m − 6 x − 8 = 0 1 x ≥ − 3
Để phương trình có hai nghiệm phân biệt thì (1) phải có 2 nghiệm phân biệt x 2 > x 1 ≥ − 3
⇔ Δ > 0 x 1 + x 2 ≥ − 6 x 1 + 3 x 2 + 3 ≥ 0 ⇔ m − 6 2 + 32 > 0 − m − 6 ≥ − 6 − 8 + 3. − m + 6 + 9 ≥ 0 ⇔ 6 − m ≥ − 6 19 − 3 m ≥ 0 ⇔ m ≤ 12 m ≤ 19 3 ⇔ m ≤ 19 3
Do đó
a b = 19 3 ⇒ a = 19 b = 3 ⇒ B = a 2 − b 3 = 19 2 − 3 3 = 334.

Đáp án B
P T ⇔ log 2 2 x 2 - x + 2 m - 4 m 2 + log 2 x 2 + m x - 2 m 2 = 0 ⇔ 2 x 2 - x + 2 m - 4 m 2 = x 2 + m x - 2 m 2 > 0 ⇔ x 2 - ( m - 1 ) x + 2 m - 2 m 2 = 0 ( x - m ) ( x + 2 m ) > 0 ⇔ [ x = 2 m x = 1 - m x - m x + 2 m > 0
Điều kiện để pt đã cho có 2 nghiệm ⇔ 4 m 2 > 0 x - m x + 2 m > 0 ⇔ m ∈ - 1 ; 1 2 \ 0
Khi đó x 1 2 + x 2 2 > 1 ⇔ 4 m 2 + 1 - m 2 > 1 ⇔ 5 m 2 - 2 m > 0 ⇔ [ m > 2 5 m < 0
Do đó S = - 1 ; 0 ∪ 2 5 ; 1 2 ⇒ A = - 1 + 2 + 1 = 2

Đáp án B
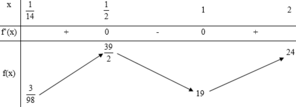
log 2 ( m x − 6 x 3 ) + log 1 2 ( − 14 x 2 + 29 x − 2 ) = 0 , ( 1 14 < x < 2 ) ⇔ log 2 ( m x − 6 x 3 ) − 14 x 2 + 29 x − 2 = 0 ⇔ m x − 6 x 3 + 14 x 2 − 29 x + 2 = 0 ⇔ 6 x 3 − 14 x 2 + 29 x − 2 x = m y = 6 x 3 − 14 x 2 + 29 x − 2 x ⇒ y ' = 12 x 3 − 14 x 2 + 2 x 2 y ' = 0 ⇔ x = − 1 3 ( L ) x = 1 2 x = 1 y ( 1 2 ) = 39 2 , y ( 1 ) = 19 ⇒ H = 39 2 − 19 = 1 2

Đáp án D
Phương pháp: Biến đổi phương trình đã cho để tính 3 x + 3 − x , từ đó thay vào biểu thức A
Cách giải:
Ta có: 9 x + 9 − x = 23
⇔ 3 x + 3 − x 2 = 25 ⇔ 3 x + 3 − x = 5 vì 3 x + 3 − x > 0 , ∀ x ∈ R
⇒ A = 5 + 3 x + 3 − x 1 − 3 x − 3 − x = 5 + 5 1 − 5 = − 5 2 = a b
Vậy a b = − 10
Chú ý khi giải:
HS thường phân vân ở chỗ tính 3 x + 3 − x vì đến đó các em không biết nhận xét 3 x + 3 − x > 0 , ∀ x dẫn đến một số em có thể chọn nhầm đáp án.


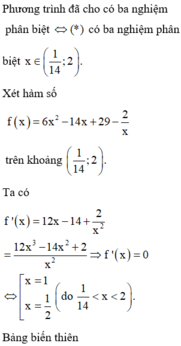


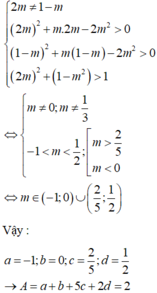
Đáp án B
Đặt t = 3 x > 0 , khi đó 9 x − 3 m .3 x + 3 m = 0 ⇔ 2 − 3 m . t + 3 m = 0 *
Để phương trình có 2 nghiệm phân biệt ⇔ * có 2 nghiệm phân biệt
⇔ Δ = 9 m 2 − 12 m > 0 t 1 + t 2 > 0 ; t 1 t 2 > 0 ⇔ 9 m 2 − 12 m > 0 3 m > 0 ⇔ m > 4 3 ⇔ m > a b → a = 4 b = 3 ⇒ b − a = − 1