Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số cách chọn 3 nút để ấn là A 10 3 = 720 .
Số trường hợp đạt yêu cầu là: (0, 1, 9); (0, 2, 8); (0, 3, 7); (0, 4, 6); (1, 2, 7); (1, 3, 6);
(1, 4, 5) ; (2, 3, 5).
Xác xuất để B mở được cửa là 8/720 = 1/90.

Để đi từ điểm tọa độ (0,0) đến tọa độ (n,m) thì cần n bước qua phải và m bước lên trên, nên cần tổng cộng \(m+n\) bước đi để đến đích.
Chọn m bước lên trên (trong tổng số \(m+n\) bước) có \(C_{m+n}^m\) cách
Còn lại n bước, chọn n cách sang phải, có \(C_n^n\) cách
Vậy tổng cộng có: \(C_{m+n}^m.C_n^n=C_{m+n}^n\) cách

Chọn C.
Giả sử số thứ tự trong danh sách là ![]()
Do dãy này là cấp số cộng nên ta có ![]()
![]() .
.
Số phần tử của không gian mẫu là n ( Ω ) = 10!
Gọi A là biến cố “Tổng các số thứ tự của hai em ngồi đối diện nhau là bằng nhau”. Để biến cố này xảy ra ta thực hiện liên tiếp các bước sau:
Bước 1: xếp thứ tự 5 cặp học sinh có các cặp số thứ tự là![]()
![]() vào trước 5 cặp ghế đối diện nhau. Bước này có 5! cách.
vào trước 5 cặp ghế đối diện nhau. Bước này có 5! cách.
Bước 2: xếp từng cặp một ngồi vào cặp ghế đối diện đã ) Chọn ở bước 1. Bước này có 2 5 cách.
Suy ra số kết quả thuận lợi cho biến cố A là 5!. 2 5 .
Vậy xác suất của biến cố A là ![]()

Phương pháp: Chia đường đi của thỏ thành 2 giai đoạn, tính số phần tử của không gian mẫu và số phần tử của biến cố A « thỏ đến được vị trí B » .
Cách giải :
Từ A đến B nhất định phải đi qua D, ta chia làm 2 giai đoạn A → D và D → B
Từ A → D có 9 cách.
Từ D → B có 6 cách tính cả đi qua C và có 3 cách không đi qua C.
Không gian mẫu n Ω = 9 . 6 = 54
Gọi A là biến cố « thỏ đến được vị trí B » thì nA = 9.3 = 27
Vậy
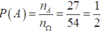




Không gian mẫu: \(C_{10}^3=120\)
Ta có 8 dãy số thỏa mãn đề bài: (0;1;9);(0;2;8);(0;3;7);(0;4;6),(1;2;7);(1;3;6);(1;4;5);(2;3;5)
Xác suất:
\(P=\dfrac{8}{120}+\left(1-\dfrac{8}{120}\right).\dfrac{8}{119}+\left(1-\dfrac{8}{120}\right).\left(1-\dfrac{8}{119}\right).\dfrac{8}{118}=...\)
Thầy ơi 119 và 118 đâu ra vậy ạ