Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Cho \(a\in R;n\in Z^+\) thì \(a^n=a\cdot a\cdot...\cdot a\)(n chữ số a)
b: \(a^0=1\)

a)
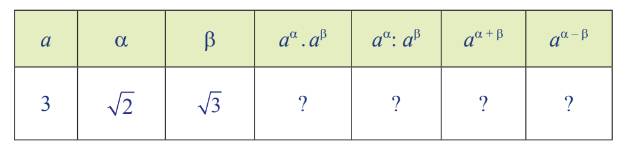
| a | α | b | \(a^{\alpha}\cdot a^{\beta}\) | \(a^{\alpha}:a^{\beta}\) | \(a^{\alpha+\beta}\) | \(\alpha^{\alpha+\beta}\) |
| 3 | \(\sqrt{2}\) | \(\sqrt{3}\) | \(3^{\sqrt{2}}\cdot3^{\sqrt{3}}=31,70659\) | \(3^{\sqrt{2}}:3^{\sqrt{3}}=0,70527\) | \(3^{\sqrt{2}+\sqrt{3}}=31,70659\) | \(3^{\sqrt{2}-\sqrt{3}}=0,70527\) |
b) Nhận xét:
\(a^m\cdot a^n=a^{m+n};a^m:a^n=a^{m-n}\)

\(a,a^{\dfrac{1}{3}}\cdot\sqrt{a}=a^{\dfrac{1}{3}}\cdot a^{\dfrac{1}{2}}=a^{\dfrac{5}{6}}\\ b,b^{\dfrac{1}{2}}\cdot b^{\dfrac{1}{3}}\cdot\sqrt[6]{b}=b^{\dfrac{1}{2}}\cdot b^{\dfrac{1}{3}}\cdot b^{\dfrac{1}{6}}=b^1\)
\(c,a^{\dfrac{4}{3}}:\sqrt[3]{a}=a^{\dfrac{4}{3}}:a^{\dfrac{1}{3}}=a^{\dfrac{4}{3}-\dfrac{1}{3}}=a\\ d,\sqrt[3]{b}:b^{\dfrac{1}{6}}=b^{\dfrac{1}{3}}:b^{\dfrac{1}{6}}=b^{\dfrac{1}{3}-\dfrac{1}{6}}=b^{\dfrac{1}{6}}=\sqrt[6]{b}\)

- Phép dời hình bảo toàn khoảng cách giữa hai điểm bất kì.
Phép đồng dạng không bảo toàn khoảng cách giữa hai điểm bất kì.
- Phép dời hình biến đường tròn thành đường tròn có bán kính không đổi.
Phép đồng dạng tỉ số k biến đường tròn bán kính R thành đường tròn bán kính k.R.
- Phép dời hình biến tam giác thành tam giác bằng nó.
Phép đồng dạng biến tam giác thành tam giác đồng dạng với nó.

a: căn bậc hai của một số a không âm là một số x thỏa mãn \(x^2=a\)
b: Căn bậc hai của một số a bất kỳ là một số x sao cho x thỏa mãn \(x^3=a\)

Giả sử trong dãy ko có lũy thừa bậc 2 của số tự nhiên nào \(\Rightarrow\) toàn bộ các số trong dãy phải nằm giữa 2 số chính phương liên tiếp
\(\Rightarrow k^2+1\le n< n+1< ...< 2n< \left(k+1\right)^2\)
\(\Rightarrow2\left(k^2+1\right)< \left(k+1\right)^2\)
\(\Leftrightarrow k^2-2k+1< 0\)
\(\Leftrightarrow\left(k-1\right)^2< 0\) (vô lý)
Vậy điều giả sử là sai hay trong dãy luôn có ít nhất 1 số là lũy thừa bậc 2 của số tự nhiên

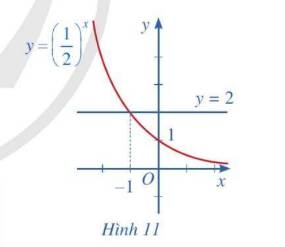
Do \(\dfrac{1}{2}< 1\) ⇒ Hàm số \(y=\left(\dfrac{1}{2}\right)^x\) nghịch biến trên R.
\(\left(\dfrac{1}{2}\right)^x>2\\ \Rightarrow x< log_{\dfrac{1}{2}}2\\ \Rightarrow x< -1\)

- Phép dời hình bảo toàn khoảng cách giữa hai điểm bất kì.
Phép đồng dạng không bảo toàn khoảng cách giữa hai điểm bất kì.
- Phép dời hình biến đường tròn thành đường tròn có bán kính không đổi.
Phép đồng dạng tỉ số k biến đường tròn bán kính R thành đường tròn bán kính k.R.
- Phép dời hình biến tam giác thành tam giác bằng nó.
Phép đồng dạng biến tam giác thành tam giác đồng dạng với nó.

a) \({\log _c}b = {\log _a}b.{\log _c}a \Leftrightarrow {a^{{{\log }_c}b}} = {a^{{{\log }_a}b.{{\log }_c}a}} \Leftrightarrow {c^{{{\log }_c}b}} = {\left( {{c^{{{\log }_c}a}}} \right)^{{{\log }_a}b}} \Leftrightarrow b = {a^{{{\log }_a}b}} \Leftrightarrow b = b\) (luôn đúng)
Vậy \({\log _c}b = {\log _a}b.{\log _c}a\)
b) Từ \({\log _c}b = {\log _a}b.{\log _c}a \Leftrightarrow {\log _a}b = \frac{{{{\log }_c}b}}{{{{\log }_c}a}}\)
\(a^m\cdot a^n=a^{m+n}\)
\(a^m:a^n=a^{m-n}\)
\(\left(a^m\right)^n=a^{m\cdot n}\)
\(\left(a\cdot b\right)^m=a^m\cdot b^m\)
\(\left(\dfrac{a}{b}\right)^m=\dfrac{a^m}{b^m}\)