Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c) *MOHD nội tiếp (cmb) \(\Rightarrow\)^DHB = ^DOM Mà ^DHM +^BHD=180 và ^DOM +^EOD =180 => ^EOD = ^BHD
Mặt khác, ^EOD =^BQD (OM // BQ) => ^BHD = ^BQD => BHQD nội tiếp.
=>đpcm
d) Kéo dài BQ cắt AC tại J
Cm Q là trung điểm BJ (đường trung bình)
Cm \(\frac{EO}{BQ}\)\(=\)\(\frac{OF}{QJ}\)(\(=\)\(\frac{AO}{AQ}\)) \(\Rightarrow\)Đpcm

Câu hỏi của TRẦN PHAN ĐỨC MINH - Toán lớp 9 - Học toán với OnlineMath

a) Xét (O) có
ΔACD nội tiếp đường tròn(A,C,D\(\in\)(O))
AD là đường kính(gt)
Do đó: ΔACD vuông tại C(Định lí)
Suy ra: AC\(\perp\)CD tại C
hay \(EC\perp CD\) tại C
Xét tứ giác ECDF có
\(\widehat{EFD}\) và \(\widehat{ECD}\) là hai góc đối
\(\widehat{EFD}+\widehat{ECD}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ECDF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
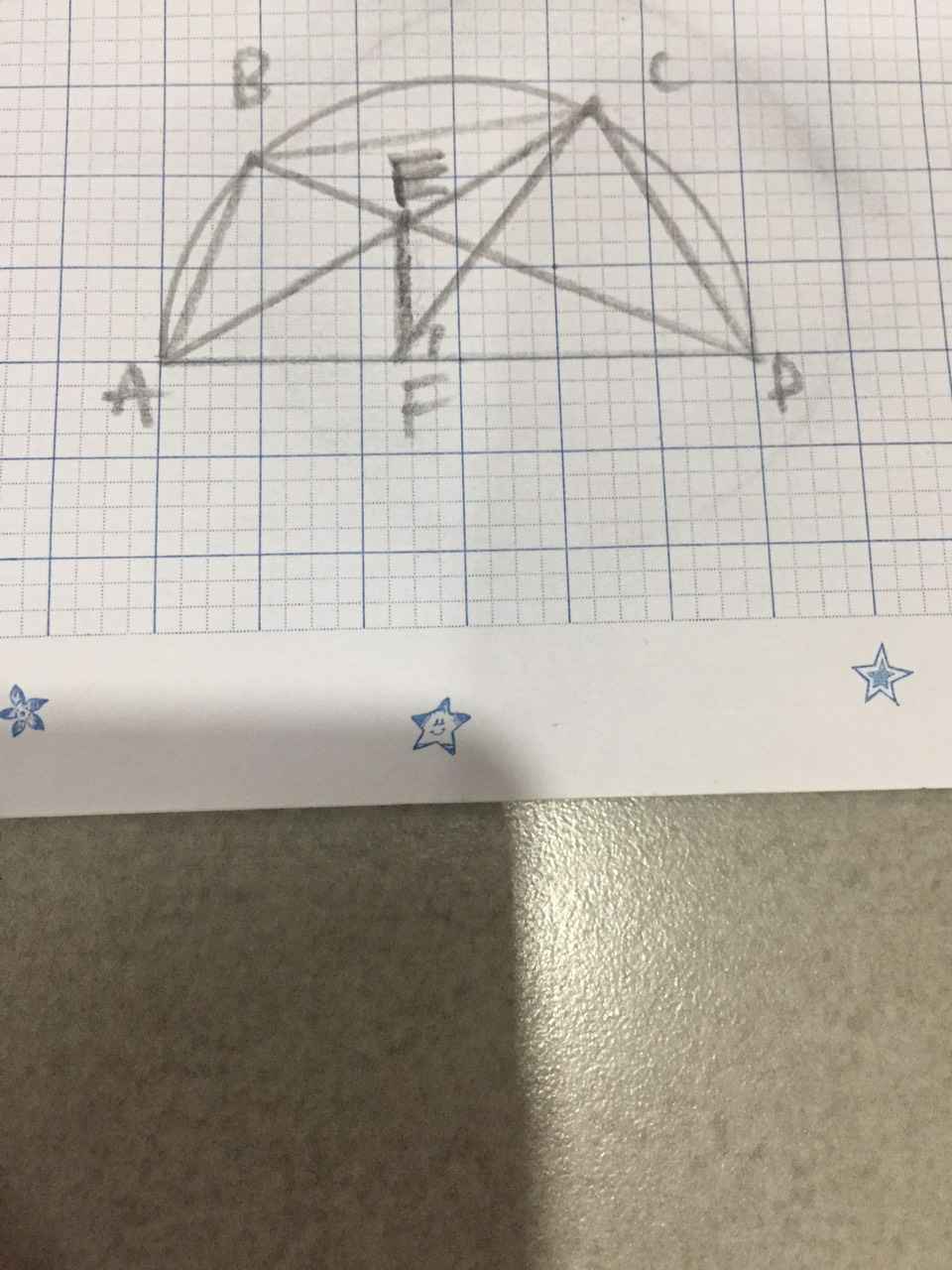

a: Xét (O) có
ΔADB nội tiếp
AB là đường kính
=>ΔADB vuông tại D
Xét (O) có
ΔACB nội tiếp
AB là đường kính
=>ΔABC vuông tại C
Xét ΔEDA vuông tại D và ΔECB vuông tại C có
góc DEA=góc CEB
=>ΔEDA đồng dạng với ΔECB
=>ED/EC=EA/EB
=>ED*EB=EC*EA
b: góc DCA=1/2*sđ cung AD
góc FCA=góc DBA=1/2*sđ cung AD
=>góc DCA=góc FCA
=>CA là phân giác của góc DCF
c: Xét ΔQAB có
QF,BD là đường cao
QF cắt BD tại E
=>E là trực tâm
=>AC vuông góc BQ
mà AC vuông góc BC
nên B,C,Q thẳng hàng
vì sao câu b góc FCA=DBA?