Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

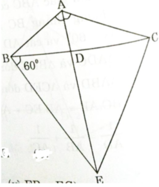
a) Xét ΔADC ∼ ΔBDE có:
∠DBE = ∠CAD ( = 60o)
∠BDE = ∠CDA (đối đỉnh)
⇒ ΔADC ∼ ΔBDE (g.g)
Xét ΔEBD và ΔEAB có:
∠BEA chung;
∠EBD = ∠BAE = 60o
⇒ ΔEBD ∼ ΔEAB (g.g)
![]()
b) Ta có ΔADC ∼ ΔBDE (cmt)
![]()
Lại có ∠ADB = ∠EDC (đối đỉnh)
Do đó ΔADB ∼ ΔCDE (c.g.c)
⇒ ∠BCE = ∠BAD = 60o
Vậy ΔEBC đều (∠EBC = ∠BCE = 60o )
c) Vì AD là phân giác của ∠BAC (gt) ta có:
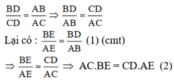
Từ (1) ta có AE.BD = BE.AB = EC.AB (vì EB = EC)
Hay EC.AB = AE.BD (3)
Công (2) và (3): AB.EC + AC.BE = AE(CD + BD) = AE.BC (đpcm)
d) Ta có: AE.BC = AB.EC + AC.BE
= AB.BC + AC.BC (vì BC = EC = BE)
= BC(AB + AC) ⇒ AE = AB + AC (*)
Mặt khác: Xét ΔADC và ΔABE có: ∠CAD = ∠BAE = 60o ; ∠ACD = ∠AEB (cmt)
⇒ ΔADC ∼ ΔABE (g.g)
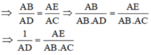
Theo (*) ta có:
![]()

a) Vì AD là tia phân giác ∠BAC => ∠BAD = ∠CAD
Mà ∠BAD = ∠CBE
Nên ∠CAD = ∠CBE
Xét ΔADC và ΔDEB có:
∠CAD = ∠CBE ( chứng minh trên )
∠ADC = ∠BDE ( đối đỉnh)
Do đó ΔADC đồng dạng với ΔDEB ( g.g)
b) Vì ΔADC đồng dạng với ΔDEB ( câu a)
=> ∠ACD = ∠BED ( 2 góc tương ứng )
Xét ΔADC có: ∠DAC + ∠DCA + ∠ADC = 180 độ
Xét ΔABE có: ∠BAE + ∠BEA + ∠ABE = 180 độ
Mà ∠DCA = ∠BEA ( chứng minh trên )
∠BAE = ∠CAD ( chứng minh trên )
=> ∠ADC = ∠ABE
c) Xét ΔABE và ΔBDE có:
∠BAE = ∠DBE ( giả thuyết)
∠E chung
Do đó ΔABE đồng dạng với ΔBDE (g.g)
=> EAEBEAEB = ABBDABBD
<=> EA . BD = EB . AB
<=>(EA . BD)² = (EB.AB)²