Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2:
a: \(D\in SD\)
\(D\in DB\subset\left(ABCD\right)\)
Do đó: \(SD\cap ABCD=D\)
b: Chọn mp(ABCD) có chứa CD
\(AB\subset\left(ABCD\right)\)
\(AB\subset\left(SAB\right)\)
Do đó: \(\left(SAB\right)\cap\left(ABCD\right)=AB\)
Gọi M là giao của AB và CD
=>\(M=CD\cap\left(SAB\right)\)
c: Chọn mp(SBD) có chứa DF
Gọi N là giao của BD và AC
\(N\in BD\subset\left(SBD\right)\)
\(N\in AC\subset\left(SAC\right)\)
Do đó: \(N\in\left(SBD\right)\cap\left(SAC\right)\)
=>\(\left(SBD\right)\cap\left(SAC\right)=SN\)
Gọi K là giao của SN với DF
=>\(K=DF\cap\left(SAC\right)\)

Để giải quyết các bài toán này, chúng ta cần sử dụng các kiến thức về hình học không gian và tính chất của các hình học trong không gian. Dưới đây là cách giải từng câu hỏi:
a) Để tìm giao điểm của SA (đường thẳng qua S và A) và mặt phẳng ABCD, chúng ta cần tìm điểm giao nhau của đường thẳng SA và mặt phẳng ABCD. Điểm giao nhau này sẽ nằm trên cạnh AD của hình chóp S.ABCD. Vì vậy, ta cần tìm điểm giao nhau của SA và AD.b) Để tìm giao điểm của BC và mặt phẳng SAD, chúng ta cần tìm điểm giao nhau của cạnh BC và mặt phẳng SAD. Điểm giao nhau này sẽ nằm trên cạnh AD của hình chóp S.ABCD. Vì vậy, ta cần tìm điểm giao nhau của BC và AD.
c) Để tìm giao điểm của AE và mặt phẳng SBD, chúng ta cần tìm điểm giao nhau của cạnh AE và mặt phẳng SBD. Điểm giao nhau này sẽ nằm trên cạnh BD của hình chóp S.ABCD. Vì vậy, ta cần tìm điểm giao nhau của AE và BD.
a) Để tìm giao điểm của SD và mặt phẳng ABCD, chúng ta cần tìm điểm giao nhau của cạnh SD và mặt phẳng ABCD. Điểm giao nhau này sẽ nằm trên cạnh AD của hình chóp S.ABCD. Vì vậy, ta cần tìm điểm giao nhau của SD và AD.b) Để tìm giao điểm của CD và mặt phẳng SAB, chúng ta cần tìm điểm giao nhau của cạnh CD và mặt phẳng SAB. Điểm giao nhau này sẽ nằm trên cạnh AB của hình chóp S.ABCD. Vì vậy, ta cần tìm điểm giao nhau của CD và AB.
c) Để tìm giao điểm của DF và mặt phẳng SAC, chúng ta cần tìm điểm giao nhau của cạnh DF và mặt phẳng SAC. Điểm giao nhau này sẽ nằm trên cạnh AC của hình chóp S.ABCD. Vì vậy, ta cần tìm điểm giao nhau của DF và AC.
Vì các bài toán này đòi hỏi tính toán chi tiết và cần biết thêm thông tin về các giá trị cụ thể của các đường thẳng và mặt phẳng, nên tôi không thể cung cấp câu trả lời chính xác mà chỉ có thể hướng dẫn cách giải quyết chúng.
1:
a: \(A\in SA\)
\(A\in\left(ABCD\right)\)
=>\(A=SA\cap\left(ABCD\right)\)
b: Gọi O là giao của AD và BC
\(O\in BC\)
\(O\in AD\subset\left(SAD\right)\)
=>\(O=BC\cap\left(SAD\right)\)
c: Chọn mp(SAC) có chứa AE
Gọi K là giao của BD và AC
\(K\in BD\subset\left(SBD\right);K\in AC\subset\left(SAC\right)\)
\(S\in SD\subset\left(SBD\right);S\in SA\subset\left(SAC\right)\)
Do đó: \(\left(SBD\right)\cap\left(SAC\right)=SK\)
Gọi F là giao của SK với AE
=>F là giao của AE với mp(SBD)

a: Trong mp(ABCD), Gọi giao của AC và BD là O
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà S thuộc (SAC) giao (SBD)
nên (SAC) giao (SBD)=SO
b:Trong mp(ABCD), Gọi giao của AB và CD là M
\(M\in AB\subset\left(SAB\right)\)
\(M\in CD\subset\left(SCD\right)\)
=>M thuộc (SAB) giao (SCD)
mà S thuộc (SAB) giao (SCD)
nên (SAB) giao (SCD)=SM
c: Trong mp(ABCD), gọi N là giao của AD với BC
\(N\in AD\subset\left(SAD\right);N\in BC\subset\left(SBC\right)\)
Do đó: \(N\in\left(SAD\right)\cap\left(SBC\right)\)
mà \(S\in\left(SAD\right)\cap\left(SBC\right)\)
nên \(\left(SAD\right)\cap\left(SBC\right)=SN\)

a: Xét hình thang ABCD có
M,N lần lượt là trung điểm của AB,CD
nên MN là đường trung bình
=>MN//AD//BC
=>MN//(SAD) và MN//(SBC)
b: Gọi giao của MN với BD là O
=>O thuộc (SBD) giao (MNP)
MP//SB
=>\(\left(SBD\right)\cap\left(MNP\right)=xy\left(O\in xy\right);\)xy//MP//SB

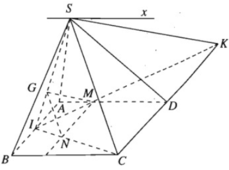
a) Dễ thấy S là một điểm chung của hai mặt phẳng (SAD) và (SBC).
Ta có:
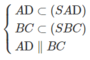
⇒ (SAD) ∩ (SBC) = Sx
Và Sx // AD // BC.
b) Ta có: MN // IA // CD
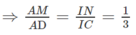
Mà 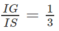
(G là trọng tâm của ∆SAB) nên
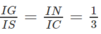 ⇒ GN // SC
⇒ GN // SC
SC ⊂ (SCD) ⇒ GN // (SCD)
c) Giả sử IM cắt CD tại K ⇒ SK ⊂ (SCD)
MN // CD ⇒
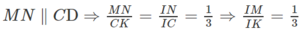
Ta có:

S A B C D M H K N O
a/
Ta có
\(S\in\left(SAD\right);S\in\left(SBC\right)\Rightarrow S\in d\) và d//AD//BC (Nếu 2 mp lần lượt chứa 2 đường thẳng // với nhau thì giao tuyến của chúng nếu có là đường thẳng // với 2 đường thẳng đã cho)
b/
Xét tg SAD có
MA=MD; HA=HS => MH là đường trung bình của tg SAD
=> MH//SD mà \(SD\in\left(SCD\right)\) => MH//(SCD) (1)
Xét tg SAB có
HA=HS; KS=KB => MH là đường trung bình của tg SAB
=> HK//AB mà AB//CD => HK//CD mà \(CD\in\left(SCD\right)\) => HK//(SCD) (2)
Từ (1) và (2) => (MHK)//(SCD) nên không có giao tuyến
c/
Gọi O là trung điểm BD, Nối MO cắt BC tại N
Xét tg ABD có
MA=MD; OB=OD => MO là đường trung bình của tg ABD
=> MO//AB; mà HK//AB (cmt) => MO//HK
=> M; O; H; K cùng thuộc mặt phẳng MKH
\(\Rightarrow MO\in\left(MKH\right)\Rightarrow MN\in\left(MKH\right)\Rightarrow N\in\left(MKH\right)\)
Mà \(N\in BC\)
=> N là giao của BC với (MKH)
Ta có MO//HK => MN//HK => MHNK là hình thang

Kéo dài AB và CD cắt nhau tại E
\(\Rightarrow SE=\left(SAB\right)\cap\left(SCD\right)\)
Qua M kẻ đường thẳng d song song CD lần lượt cắt AC và AD tại F và G
Trong mp (SAC), qua F kẻ đường thẳng song song SA cắt SC tại P
Trong mp (SAD), qua G kẻ đường thẳng song song SA cắt SD tại Q
\(\Rightarrow\) Hình thang MPQG là thiết diện của (P) và chóp

a: \(O\in BD\subset\left(SBD\right)\)
\(O\in AC\subset\left(SAC\right)\)
=>\(O\in\left(SBD\right)\cap\left(SAC\right)\)
=>\(\left(SBD\right)\cap\left(SAC\right)=SO\)
b: \(S\in\left(SAB\right)\cap\left(SCD\right)\)
AB//CD
=>(SAB) giao (SCD)=xy, xy đi qua S và xy//AB//CD
c: \(S\in\left(SAD\right)\cap\left(SBC\right)\)
AD//BC
Do đó: (SAD) giao (SBC)=mn, mn đi qua S và mn//AD//BC
d: \(CD\subset\left(HKCD\right)\)
\(CD\subset\left(ABCD\right)\)
Do đó: (HKCD) giao (ABCD)=CD


a: Trong mp(ABCD), gọi N là giao điểm của AD và BC
\(N\in AD\subset\left(SAD\right);N\in BC\subset\left(SBC\right)\)
=>\(N\in\left(SAD\right)\cap\left(SBC\right)\)
mà \(S\in\left(SAD\right)\cap\left(SBC\right)\)
nên \(\left(SAD\right)\cap\left(SBC\right)=SN\)
b: Gọi H là giao điểm của SG với CD
Xét ΔSCD có
G là trọng tâm
H là giao điểm của SG với DC
Do đó: H là trung điểm của DC
Chọn mp(SAH) có chứa MG
Trong mp(ABCD), gọi E là giao điểm của AH với BD
\(E\in AH\subset\left(SAH\right)\)
\(E\in BD\subset\left(SBD\right)\)
Do đó: \(E\in\left(SAH\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAH\right)\cap\left(SBD\right)\)
nên \(\left(SAH\right)\cap\left(SBD\right)=SE\)
Gọi K là giao điểm của MG với SE
=>K là giao điểm của MG với (SBD)