Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

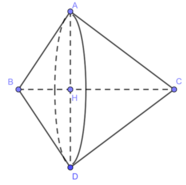
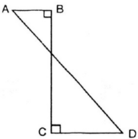
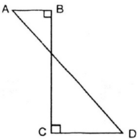
Nếu gọi O là giao điểm của BC và AD. Khi quay hình ABCD quanh BC thì có nghĩa là quay tam giác vuông OAB quanh OB và tam giác vuông OCD quanh OC. Mỗi hình quay sẽ tạo ra một hình nón. Vậy hình tạo ra sẽ là hai hình nón.
Vậy chọn D.
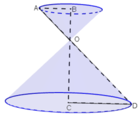

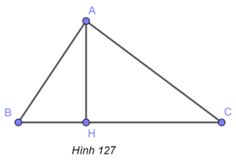
Khi quay tam giác ABC quanh cạnh BC cố định ta sẽ được hai hình nón có chung hình tròn đáy như hình bên .
Đáp án: (B)

Bạn kiểm tra lại đề bài? S max thì S là diện tích xung quanh hay diện tích toàn phần ạ. Hay là V max vậy?
Mình làm S xung quanh max nhé!
Không vẽ được hình. Bạn thông cảm:
+) Gọi chiều cao của hình trụ là: h' ; bán kính đáy là r'
Áp dụng định lí ta - let ta có: \(\frac{h'}{h}=\frac{r-r'}{r}=1-\frac{r'}{r}\)
<=> \(\frac{h'}{18}=1-\frac{r'}{9}\)
<=> \(h'=18-2r'\)
Công thức tính xung quanh của hình trụ:
\(S_{xq}=2\pi r'h'=2\pi r'\left(18-2r'\right)=-4.\pi r'^2+36.\pi r'\)
\(=-4\pi\left(r'^2-9r+\frac{81}{4}\right)+81\pi\)
\(=-4\pi\left(r'-\frac{9}{2}\right)^2+81\pi\le81\pi\)
=> S toàn phần max = 81 pi
khi đó: r' = 9/2 và h' = 9

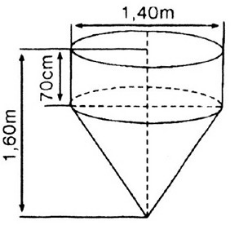
Giải: a) Thể tích cần tính gồm một hình trụ, đường kính đáy 1,4m, chiều cao 70cm, và một hình nón, bán kính đáy bằng bán kính hình trụ, chiều cao hình nón bằng 0,9m.
Thể tích hình trụ: Vtrụ = πR2h = 3,14. . 0.7 ≈ 1,077 (m3)
Thể tích hình nón: Vnón = (1/3). 3,14. .0,9 = 0,462 (m3)
Vậy thể tích cái phễu:
V = Vtrụ + Vnón = 1,077 + 0,462 = 1,539 (m3)
b) Diện tích cần tính gồm diện tích xung quanh hình trụ và diện tích xung quanh hình nón. Đường sinh của hình nón là:
Sxq trụ = 2πrh = 2.3,14.. 0,7= 3,077 (m2)
S xq nón = πrl = 3,14..1,4 = 2,506 (m2)
Vậy diện tích toàn phần của phễu:
S= Sxq trụ + S xq nón = 3,077 + 2,506 = 5,583 (m2)

Giải
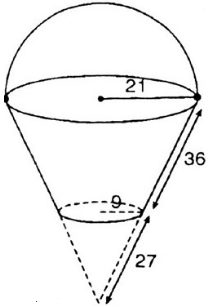
a) Diện tích cần tính gồm diện tích xung quanh của hình xung quanh của hình nón cụt và diện tích hình tròn đáy có bán kính 9cm.
Đường sinh của hình nón lớn là l = 36 + 27 = 63 cm.
Diện tích xung quanh của hình nón lớn, hình nón nhỏ:
S xq nón lớn = πrl = 3,14.21.63 =4154,22 (cm2)
S xq nón nhỏ = 3,14.9.27 =763,02 (cm2)
Diện tích xung quanh của hình nón cụt:
S xq nón cụt = S xq nón lớn -S xq nón nhỏ = 4154,22 - 763,02 = 3391,2 (cm2)
Diện tích hình tròn đáy:
Shình tròn đáy = 2 = 3,14.92 = 254,34 (cm2)
Diện tích mặt ngoài của xô:
S = S xq nón cụt + Shình tròn đáy = 3391,2 + 254,34 = 3645,54 (cm2)
b) Chiều cao của hình nón lớn:
h= = 59,397 (cm)
Chiều cao của hình nón nhỏ:
h' = = 25,546 (cm)
Thể tích của hình nón lớn:
Vhình tròn lớn = (1/3)πrh = (1/3). 3,14.212.59,397 = 27416,467 (cm3)
Thể tích hình nón nhỏ:
Vhình tròn nhỏ = (1/3)πrh = (1/3). 3,14.92.25,456 = 2158,160 (cm3)
Khi xô chứa đầy hóa chất thì dung tích của nó là:
V= Vhình tròn lớn -Vhình tròn nhỏ = 27416,467 - 2158,160 = 25258 (cm3)
= 25,3 (dm3)

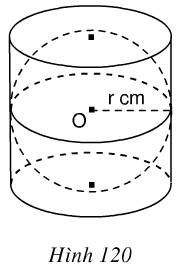
Hình 120 mô tả một hình cầu được đặt khít vào trong một hình trụ, các kích thước cho trên hình vẽ.
Hãy tính:
a)Thể tích hình cầu.
b) Thể tích hình trụ.
c) Hiệu giữa thể tích hình trụ và thể tích hình cầu.
d) Thể tích của một hình nón có bán kính đường tròn đáy là r cm và chiều cao 2r cm.
e) Từ các kết quả a), b), c), d) hãy tìm mối liên hệ giữa chúng.
Hướng dẫn trả lời:
a) Thể tích của hình cầu là:
V1=43πr3(cm3)V1=43πr3(cm3)
b) Thể tích hình trụ là:
V2 = πr2. 2r = 2πr3 (cm3)
c) Hiệu giữa thể tích hình trụ và thể tích hình cầu là:
V3=V2−V1=2πr3−43πr2=23πr3(cm3)V3=V2−V1=2πr3−43πr2=23πr3(cm3)
d) Thể tích hình nón là:
V4=π3r2.2r=23πr3(cm3)V4=π3r2.2r=23πr3(cm3)
e) Từ kết quả ở câu s, b,c, d ta có hệ thức: V4 = V2 – V1 hay “ Thể tích hình nón nội tiếp trong hình trụ bằng hiệu giữa thể tích hình trụ và thể tích hình cầu nội tiếp trong hình trụ ấy”

Hướng dẫn trả lời:
a) Thể tích của hình cầu là:
V1=43πr3(cm3)V1=43πr3(cm3)
b) Thể tích hình trụ là:
V2 = πr2. 2r = 2πr3 (cm3)
c) Hiệu giữa thể tích hình trụ và thể tích hình cầu là:
V3=V2−V1=2πr3−43πr2=23πr3(cm3)V3=V2−V1=2πr3−43πr2=23πr3(cm3)
d) Thể tích hình nón là:
V4=π3r2.2r=23πr3(cm3)V4=π3r2.2r=23πr3(cm3)
e) Từ kết quả ở câu s, b,c, d ta có hệ thức: V4 = V2 – V1 hay “ Thể tích hình nón nội tiếp trong hình trụ bằng hiệu giữa thể tích hình trụ và thể tích hình cầu nội tiếp trong hình trụ ấy”

Hướng dẫn trả lời:
Hình a.
V=π(12,62)2.8,4+12.43π(12,62)3=13π(6,9)2.(8,4+12,63)=500,094π(cm3)V=π(12,62)2.8,4+12.43π(12,62)3=13π(6,9)2.(8,4+12,63)=500,094π(cm3)
Vậy Vhình a = 500,094π cm3
Hình b.
V=13π(6,9)2.20+12.43π.(6,9)3=13π(6,9)2(20+13,8)=536,406π(cm3)V=13π(6,9)2.20+12.43π.(6,9)3=13π(6,9)2(20+13,8)=536,406π(cm3)
Vậy Vhình b = 536, 406π cm3
Hình c.
V=13π.22.4+π.22.4+12.43π.23=4.22.π(13+1+13)=80π3(cm3)V=13π.22.4+π.22.4+12.43π.23=4.22.π(13+1+13)=80π3(cm3)
Vậy Vhình c =
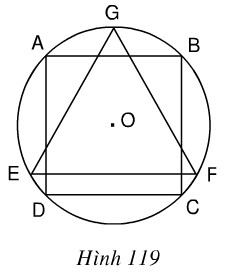
Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (h.119). Cho hình đó quay quanh trục GO. Chứng minh rằng:
a) Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh ra.
b) Bình phương diện tích toàn phần của hình trụ bằng tích của diện tích hình cầu và diện tích toàn phần của hình nón.
Hướng dẫn trả lời:
a) Thể tích hình trụ được tạo bởi hình vuông ABCD là:
V=π(AB2)2.BCV=π(AB2)2.BC với AB là đường chéo của hình vuông có cạnh là R và AB = R√2 (=BC)
V=π(R√22)2.R√2=π.2R24.R√2=πR3√22⇒V2=(πR3√222)=2π2R62(1)V=π(R22)2.R2=π.2R24.R2=πR322⇒V2=(πR3222)=2π2R62(1)
Thể tích hình cầu có bán kính R là: V1=43πR3V1=43πR3
Thể tích hình nón có bán kính đường tròn đáy bằng EF2EF2 là:
V2=13π(EF2)2.GHV2=13π(EF2)2.GH
Với EF = R√3 (cạnh tam giác đều nội tiếp trong đường tròn (O;R))
và GH=EF√32=R√3.√32=3R2GH=EF32=R3.32=3R2
Thay vào V2, ta có: V2=13π(R√32)2.3R2=38πR3V2=13π(R32)2.3R2=38πR3
Ta có: V1V2=43πR3.38πR3=π2R62(2)V1V2=43πR3.38πR3=π2R62(2)
So sánh (1) và (2) ta được : V2 = V1. V2
b) Diện tích toàn phần của hình trụ có bán kính AB2AB2 là:
S=2π(AB2).BC+2π(AB2)2S=2π.R√22R√2+2π(R√22)2S=2πR2+πR2=3πR2⇒S2=(3πR2)2=9π2.R4(1)S=2π(AB2).BC+2π(AB2)2S=2π.R22R2+2π(R22)2S=2πR2+πR2=3πR2⇒S2=(3πR2)2=9π2.R4(1)
Diện tích mặt cầu có bán kính R là: S1 = 4πR2 (2)
Diện tích toàn phần của hình nón là:
S2=πEF2.FG+π(EF2)2=πR√32.R√3+π(R√32)2=9πR24S2=πEF2.FG+π(EF2)2=πR32.R3+π(R32)2=9πR24
Ta có: S1S2=4πR2.9πR24=9π2R4(2)S1S2=4πR2.9πR24=9π2R4(2)
So sánh (1) và (2) ta có: S2 = S1. S2

-0133-1.jpg)
-0132.jpg)
Nếu gọi O là giao điểm của BC và AD. Khi quay hình ABCD quanh BC thì có nghĩa là quay tam giác vuông OAB quanh OB và tam giác vuông OCD quanh OC. Mỗi hình quay sẽ tạo ra một hình nón. Vậy hình tạo ra sẽ là hai hình nón.
Vậy chọn D.