Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

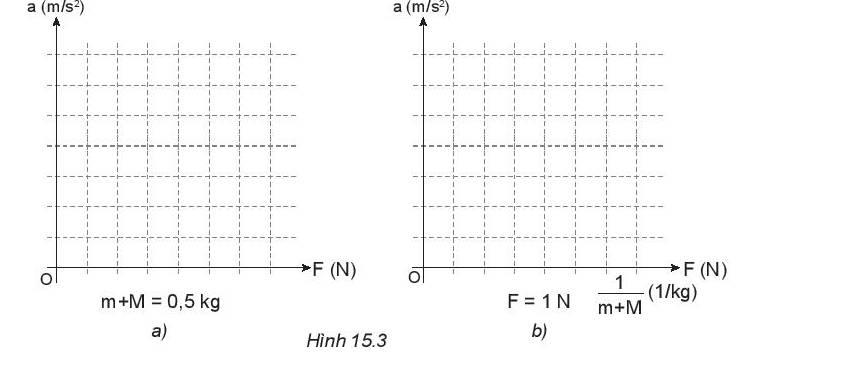
a)
- a phụ thuộc vào F (m + M = 0, 5kg)
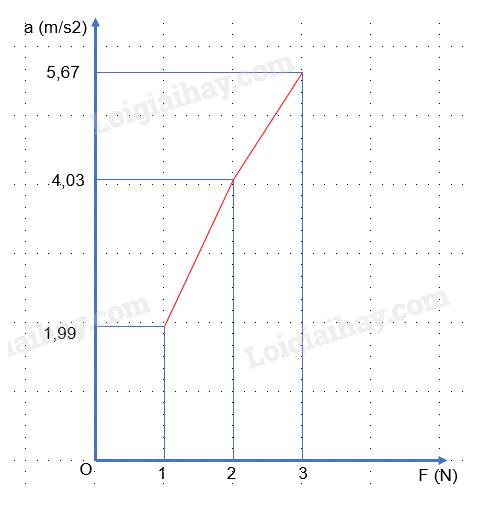
Ta có:
+ Khi F = 1 N, a = 1,99 m/s2 thì \(\frac{F}{a} = \frac{1}{{1,99}} \approx 0,5\)
+ Khi F = 2 N, a = 4,03 m/s2 thì \(\frac{F}{a} = \frac{2}{{4,03}} \approx 0,5\)
+ Khi F = 3 N, a = 5,67 m/s2 thì \(\frac{F}{a} = \frac{3}{{5,67}} \approx 0,5\)
=> Tỉ số \(\frac{F}{a}\) không đổi nên đồ thị sự phụ thuộc của gia tốc a vào F là một đường thẳng
- a phụ thuộc vào \(\frac{1}{{m + M}}\) (ứng với F = 1 N)
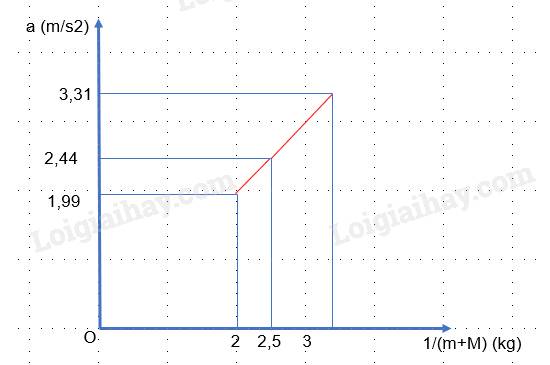
Ta có:
+ Khi a = 3,31 m/s2 , \(\frac{1}{{M + m}} = \frac{{10}}{3}\) thì a. (M + m) = 1
+ Khi a = 2,44 m/s2 , \(\frac{1}{{M + m}} = 2,5\) thì a. (M + m) = 1
+ Khi a = 1,99 m/s2 , \(\frac{1}{{M + m}} = 2\) thì a. (M + m) = 1
=> Tỉ số \(\frac{a}{{\frac{1}{{M + m}}}} = a.(M + m)\) không đổi nên đồ thị sự phụ thuộc của gia tốc a vào \(\frac{1}{{M + m}}\) là một đường thẳng.
b) Ta có:
+ Khi (m + M) không đổi, F tăng thì a cũng tăng => Gia tốc a tỉ lệ thuận với lực F
+ Khi F không đổi, a giảm thì (m+M) tăng => Gia tốc a tỉ lệ nghịch với khối lượng
=> Kết luận: Gia tốc tỉ lệ thuận với lực tác dụng và tỉ lệ nghịch với khối lượng.

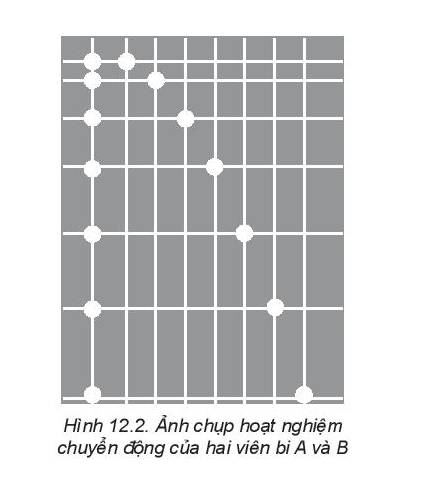
Thông qua quan sát, ta thấy tọa độ tính theo phương ngang của hai viên bi A và viên bi B đều không thay đổi, và đều trong cùng một khoảng thời gian
Mặt khác, ta có \(v=\dfrac{s}{t}=\dfrac{x}{t}\)
(do vật không đổi chiều chuyển động). Tọa độ x không đổi, thời gian như nhau, nên vận tốc không thay đổi
\(\Rightarrow v_x=v_0\)
Theo em, có thể có 30 phần trăm động năng của thác nước được nhà máy thủy điện chuyển hóa thành điện năng.
Cũng tùy thuộc vào công suất của từng nhà máy.

1. (a)
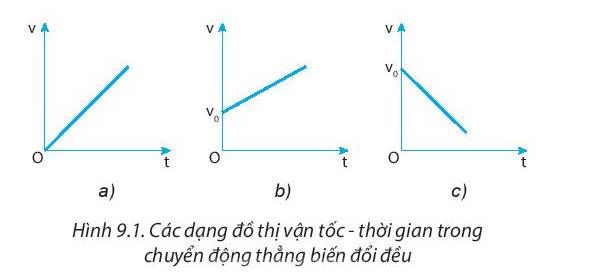
Đồ thị hình a là đường thẳng đi qua gốc tọa độ nên công thức mối liên hệ giữa v, a và t có dạng hàm số \(y=ax\). Công thức cần tìm là: \(v=at\left(a>0\right)\).
Đồ thị hình b là đường thẳng xuất phát từ điểm \(v_0\) cách gốc tọa độ một khoảng đúng bằng \(v_0\) nên công thức mối liên hệ có dạng hàm số \(y=ax+b\left(a>0\right)\) (do đồ thị có dạng dấu sắc (đồng biến)) nên công thức cần tìm là: \(v=v_0+at\).
Đồ thị hình b là đường thẳng xuất phát từ điểm \(v_0\) cách gốc tọa độ một khoảng đúng bằng \(v_0\) nên công thức mối liên hệ có dạng hàm số \(y=ax+b\left(a< 0\right)\) (do đồ thị có dạng dấu huyền (nghịch biến)) nên công thức cần tìm là: \(v=v_0-at\).
(b) Chuyển động nhanh dần đều là các chuyển động ở hình a, b. Chuyển động chậm dần đều là chuyển động ở hình c.
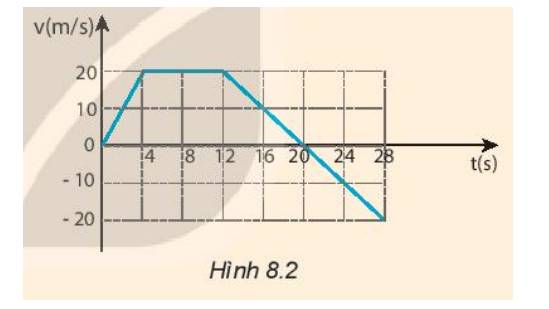
2. Từ thời điểm 0s đến 4s, tức 4s đầu, bạn đi đều với tốc độ 1,5m/s.
Từ thời điểm 4s đến 6s, tức 2s tiếp theo, bạn bắt đầu đi chậm lại từ tốc độ 1,5m/s xuống 0m/s.
Sau đó, từ thời điểm 6s đến 7s, tức 1s tiếp theo, bạn này dừng lại.
Trong 1s tiếp theo, từ thời điểm 7s đến 8s, bạn này bắt đầu đảo chiều đi (đi ngược lại so với chiều đi ban đầu) và bắt đầu chuyển động nhanh dần từ tốc độ 0m/s đến 0,5m/s.
Trong 1s sau đó, từ thời điểm 8s đến 9s, bạn này đi đều với tốc độ 0,5m/s với chiều đi như giây trước.
Cuối cùng, từ thời điểm 9s đến 10s, tức 1s cuối, bạn này đi chậm lại từ tốc độ 0,5m/s và dừng hẳn (tốc độ 0m/s).

- Mô tả hoạt động:
Khi bắt đầu, động cơ điện từ từ kéo toa tàu lên đỉnh đầu tiên của cung đường ray. Sau đó, toa tàu trượt xuống và tăng tốc, nó chuyển động nhanh dần và có đà để di chuyển đến đỉnh thứ hai (thấp hơn đỉnh thứ nhất); sau đó tiếp tục trượt xuống và tăng tốc.
Lực kéo của động cơ thực hiện công đưa toa tàu lên đỉnh đường ray, dự trữ thế năng cực đại. Khi toa tàu này trượt xuống, động năng của nó tăng và đồng thời thế năng của nó giảm. Khi tới đáy của cung đường, toàn bộ thế năng đã chuyển hóa thành động năng, năng lượng nhiệt và năng lượng âm thanh. Khi lên dốc, động năng của toa tàu giảm, chuyển hóa thành thế năng.
Giải thích tại sao khi tàu lượn ở vị trí cao nhất của đường ray thì tốc độ của nó lại chậm nhất và ngược lại.
- Khi tàu lượn ở vị trí cao nhất của đường ray, tàu lượn có thể năng trọng trường lớn nhất, động năng nhỏ nhất nên tốc độ của nó chậm nhất. Còn khi tàu lượn ở vị trí thấp nhất của đường ray, tàu lượn có thế năng trọng trường nhỏ nhất, động năng lớn nhất nên tốc độ của nó nhanh nhất.

1.
a) Đổi 5 km/h = \(\frac{{25}}{{18}}\)m/s; 29 km/h = \(\frac{{145}}{{18}}\)m/s; 49 km/h = \(\frac{{245}}{{18}}\); 30 km/h = \(\frac{{25}}{3}\)m/s
+ Gia tốc trong đoạn đường 1: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{25}}{{18.1}} = \frac{{25}}{{18}} \approx 1,39(m/{s^2})\)
+ Gia tốc trong đoạn đường 2: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{\frac{{145}}{{18}} - \frac{{25}}{{18}}}}{{4 - 1}} \approx 2,22(m/{s^2})\)
+ Gia tốc trong đoạn đường 3: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{\frac{{245}}{{18}} - \frac{{145}}{{18}}}}{{6 - 4}} \approx 2,78(m/{s^2})\)
+ Gia tốc trong đoạn đường 4: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{\frac{{25}}{3} - \frac{{245}}{{18}}}}{{7 - 6}} \approx - 5,28(m/{s^2})\)
b) Trong 4 đoạn đường trên, vận tốc tăng dần, còn gia tốc từ đoạn đường 1 đến đoạn đường 3 tăng dần, nhưng từ đoạn đường 3 đến đoạn đường 4 thì gia tốc giảm dần.
2.
Gia tốc của con báo là:
\(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{9 - 30}}{3} = - 7(m/{s^2})\)

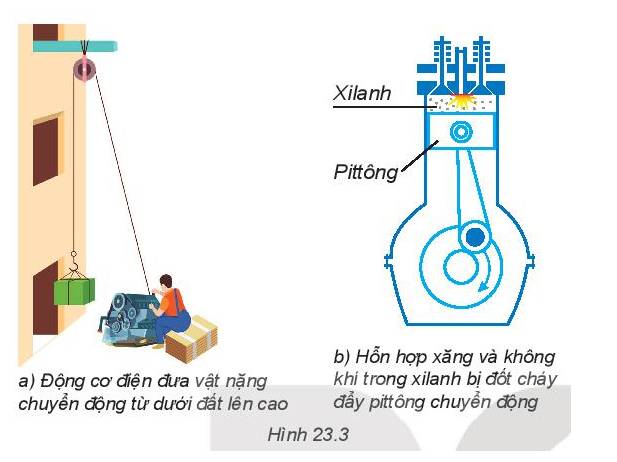
a) Động cơ điện đưa vật nặng chuyển động từ dưới đất lên cao
Khi kéo vật lên cao, lực kéo đã làm vật từ trạng thái đứng yên (v = 0; Wđ = 0) sang trạng thái chuyển động (vận tốc tăng, động năng tăng). Động năng của vật nhận được năng lượng từ lực kéo của ròng rọc truyền sang.
=> Đã có sự truyền năng lượng bằng cách thực hiện công.
b) Hỗn hợp xăng và không khí trong xilanh bị đốt cháy đẩy pittông chuyển động.
Khi đốt cháy, pittông chuyển động, chứng tỏ nhiệt năng đã chuyển hóa thành động năng. Động năng của pittông nhận được là do pittông đã nhận được năng lượng nhiệt từ xilanh.
=> Đã có sự truyền năng lượng bằng cách thực hiện công.

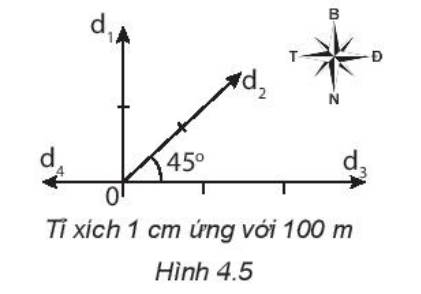
Độ dịch chuyển mô tả trên Hình 4.5 là:
+ d1 = 200 m (Bắc)
+ d2 = 200 m (Đông Bắc)
+ d3 = 300 m (Đông)
+ d4 = 100 m (Tây).

Khi xe mô tô đua vào khúc cua thì bộ phận của xe chuyển động tròn là: bánh xe.









Chọn mốc thế năng tại mặt đất
Khi vận động viên trượt từ đỉnh máng xuống chân máng, độ cao giảm và vận tốc tăng nên thế năng giảm và động năng tăng
Nhưng khi từ chân máng lên đến đỉnh máng thì độ cao tăng và vận tốc giảm nên thế năng tăng và động năng giảm
Khi bỏ qua mọi ma sát thì cơ năng của vận động này được bảo toàn.