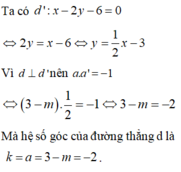K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 2 2020
Câu 6 :
Ta có hệ phương trình : \(\left\{{}\begin{matrix}x+2y=n\left(I\right)\\2x-3y=5\left(II\right)\end{matrix}\right.\)
- Từ ( I ) ta có phương trình :\(x+2y=n\)
=> \(x=n-2y\left(III\right)\)
- Thay x = n - 2y vào phương trình (II ) ta được : \(2\left(n-2y\right)-3y=5\)
=> \(2n-4y-3y=5\)
=> \(-7y=5-2n\)
=> \(y=\frac{5-2n}{-7}=\frac{2n-5}{7}\)
- Thay \(y=\frac{2n-5}{7}\) vào phương trình ( III ) ta được : \(x=n-\frac{2\left(2n-5\right)}{7}\)
=> \(x=\frac{7n}{7}-\frac{4n-10}{7}\)
=> \(x=\frac{3n-10}{7}\)
Ta có : \(\left\{{}\begin{matrix}x< 0\\y>0\end{matrix}\right.\) ( IV )
- Thay \(x=\frac{3n-10}{7}\), \(y=\frac{2n-5}{7}\) vào hệ bất phương trình ( IV ) ta được : \(\left\{{}\begin{matrix}\frac{3n-10}{7}< 0\\\frac{2n-5}{7}>0\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}3n-10< 0\\2n-5>0\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}3n< 10\\2n>5\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}n< \frac{10}{3}\\n>\frac{5}{2}\end{matrix}\right.\)
=> \(\frac{5}{2}< n< \frac{10}{3}\)
Vậy để phương trình trên có nghiệm (x, y ) thỏa mãn x <0, y > 0 thì \(\frac{5}{2}< n< \frac{10}{3}\)
25 tháng 11 2022
Bài 2:
a: (d): y=ax+b
Theo đề, ta có:
\(\left\{{}\begin{matrix}a\sqrt{2}+b=1\\a\cdot0+b=3\sqrt{2}+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=3\sqrt{2}+1\\a=\dfrac{1-b}{\sqrt{2}}=\dfrac{1-3\sqrt{2}-1}{\sqrt{2}}=-3\end{matrix}\right.\)
b: Tọa độ giao của (d1) và (d2) là:
2/5x+1=-x+4 và y=-x+4
=>7/5x=3và y=-x+4
=>x=15/7 và y=-15/7+4=13/7
Vì (d) đi qua B(15/7;13/7) và C(1/2;-1/4)
nên ta có hệ:
15/7a+b=13/7 và 1/2a+b=-1/4
=>a=59/46; b=-41/46
NN
2
CM
11 tháng 8 2017
Đáp án D
Ta có hai đường thẳng d: y = (2m - 4)x + 5 và d': 2x - y - 3 = 0 hay d': y = 2x - 3
Mà d // d' ⇒ 2m - 4 = 2 (1)
Mặt khác, d có hệ số góc là 2m – 4 và d’ có hệ số góc là 2 (2)
Từ (1) và (2) ⇒ hệ số góc của d là 2