Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
) mà các điểm đầu và điểm cuối được lấy từ các điểm phân biệt đã cho trong các trường hợp sau đây:
là vectơ nào? Vectơ đối của vectơ 
là vectơ nào?
có tâm là O. Tìm các vectơ từ 5 điểm A, B, C, D, O
; 
b) Có độ dài bằng 
và 
sao cho 
, 
. Chứng minh rằng 
là trung điểm của 
.
, 
. Chứng minh rằng 
.
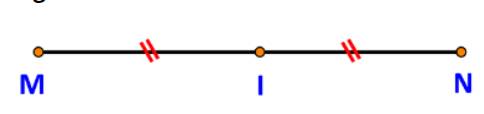
a) Các vectơ đó là: \(\overrightarrow {MI} ,\overrightarrow {IM} ,\overrightarrow {IN} ,\overrightarrow {NI} ,\overrightarrow {MN} ,\overrightarrow {NM} \).
b) Dễ thấy:
+) vectơ \(\overrightarrow {IN} \)cùng hướng với vectơ \(\overrightarrow {MI} \). Hơn nữa: \(|\overrightarrow {IN} |\; = IN = MI = \;|\overrightarrow {MI} |\)
\( \Rightarrow \overrightarrow {IN} = \overrightarrow {MI} \)
+) vectơ \(\overrightarrow {IM} \)cùng hướng với vectơ \(\overrightarrow {NI} \). Hơn nữa: \(|\overrightarrow {IM} |\; = IM = NI = \;|\overrightarrow {NI} |\)
\( \Rightarrow \overrightarrow {IM} = \overrightarrow {NI} \)
Vậy \(\overrightarrow {IN} = \overrightarrow {MI} \) và \(\overrightarrow {IM} = \overrightarrow {NI} \).
\(\overrightarrow {AB} = \overrightarrow a \;\;\, \Rightarrow \left\{ \begin{array}{l}AB//\;a\\AB = a\end{array} \right.\) và \(\overrightarrow {A'B'} = \overrightarrow a \;\;\, \Rightarrow \left\{ \begin{array}{l}A'B'\;//\;a\\A'B' = a\end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}AB//\;A'B'\\AB = A'B'\end{array} \right.\)
Tương tự, ta cũng suy ra \(\left\{ \begin{array}{l}BC//\;B'C'\\BC = B'C'\end{array} \right.\)
\( \Rightarrow \Delta ABC = \Delta A'B'C'\)(c-g-c)
\(\left\{ \begin{array}{l}AC//\;A'C'\\AC = A'C'\end{array} \right.\)
Dễ dàng suy ra \(\overrightarrow {AC} = \overrightarrow {A'C'} \).
Có thể tạo được 6 vecto theo yêu cầu đó là: \(\overrightarrow {AB} ,\overrightarrow {BA} ,\overrightarrow {AC} ,\overrightarrow {CA} ,\overrightarrow {BC,} \overrightarrow {CB} \)
Tham khảo:
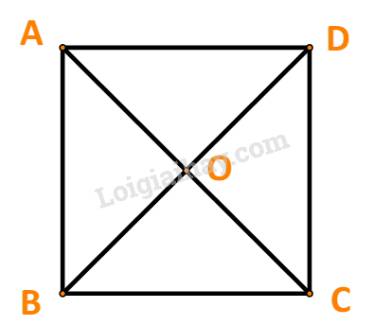
Tập hợp S là: \(S = \{ \overrightarrow {AB} ;\;\overrightarrow {AC} ;\;\overrightarrow {AD} ;\;\overrightarrow {AO} ;\;\overrightarrow {BA} ;\;\overrightarrow {BC} ;\;\overrightarrow {BD} ;\;\overrightarrow {BO} ;\;\overrightarrow {CB} ;\;\overrightarrow {CA} ;\;\overrightarrow {CD} ;\;\overrightarrow {CO} ;\;\overrightarrow {DB} ;\;\overrightarrow {DC} ;\;\overrightarrow {DA} ;\;\overrightarrow {DO} ;\;\overrightarrow {OB} ;\;\overrightarrow {OC} ;\;\overrightarrow {OD} ;\;\overrightarrow {OA} \} \)
Các nhóm trong S là:
\(\begin{array}{l}\{ \overrightarrow {AB} ;\overrightarrow {DC} \} ,\{ \overrightarrow {BA} ;\overrightarrow {CD} \} ,\{ \overrightarrow {AD} ;\overrightarrow {BC} \} ,\{ \overrightarrow {DA} ;\overrightarrow {CB} \} ,\\\{ \overrightarrow {AO} ;\overrightarrow {OC} \} ,\{ \overrightarrow {OA} ;\overrightarrow {CO} \} ,\{ \overrightarrow {OB} ;\overrightarrow {DO} \} ,\{ \overrightarrow {BO} ;\overrightarrow {OD} \} .\end{array}\)
a) Có hai véc tơ.
b) A B C A B C
Số đoạn thẳng tạo thành từ 3 điểm A, B, C là:\(\dfrac{3.2}{2}=3\) đoạn.
Mỗi đoạn thẳng tạo thành hai véc tơ đối nhau nên số véc tơ là:
\(3.2=6\) (véc tơ).
b) Số đoạn thẳng tạo thành từ 4 điểm phân biệt là:
\(4.3:2=6\) (đoạn).
Số véc tơ tạo thành là:
6.2 = 12 (véc tơ).