Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho tam giác ABC vuông tại A, AB<AC. Trung tuyến AM, ˆACB=x,ˆAMB=yACB^=x,AMB^=yChứng minh (sin x +cos x)2=1+sin y
MÌNH CẦN GẤP MỌI NGƯỜI GIÚP MÌNH NHA

đường kính của trái đất : 6400x2=12800km
bán kính của vệ tinh=đường kính trái đất + khoảng cách của vệ tinh so với trái đất=12800+35768=46568km
đường kính=2 x bán kính=2x46568=97136km

a) Khoảng cách giữa 2 vị trí đó là :
\(\frac{20000}{180}.\left(72-42\right)\simeq2800\left(km\right)\)
b) Bán kính của Trái Đất là :
\(\frac{20000}{3,14}\simeq6400\left(km\right)\)
Độ dài đường xích đạo là :
\(20000.2=40000\left(km\right)\)
Vì trái đất là hình cầu :
Thể tích hình cầu được tính dưới dạng : \(V=\frac{4}{3}.3,14.R^3\)( R là bán kính )
Vậy thể tích Trái Đất là :
\(\frac{4}{3}.3,14.\left(6400\right)^3\simeq1097509547000\left(km^3\right)\)

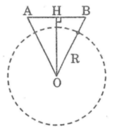
Vì hai vệ tinh cùng cách mặt đất 230 km nên tam giác AOB cân tại O.
Ta có: OA = R + 230
= 6370 + 230 = 6600 (km)
Trong tam giác AOB ta có: OH ⊥ AB
Suy ra: HA = HB = AB/2 = 2200/2 = 1100 (km)
Áp dụng định lí Pi-ta-go vào tam giác vuông AHO, ta có:
O A 2 = A H 2 + O H 2
Suy ra: O H 2 = O A 2 - A H 2
Suy ra:
OH = ![]() ≈ 6508 (km)
≈ 6508 (km)
Vì OH > R nên hai vệ tinh nhìn thấy nhau.

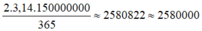 (km)
(km)