Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử hai dao động có phương trình tổng quát là:
\(\left\{{}\begin{matrix}x_1=A_1cos\left(\omega t+\varphi_1\right)\\x_2=A_2cos\left(\omega t+\varphi_2\right)\end{matrix}\right.\)
Độ lệch pha giữa hai dao động là: \(\Delta\varphi=\left(\omega t+\varphi_2\right)-\left(\omega t+\varphi_1\right)=\varphi_2-\varphi_1\)

Độ lệch pha là đại lượng đặc trưng cho độ lệch về thời gian giữa hai dao động điều hoà cùng chu kì.
Chọn D.

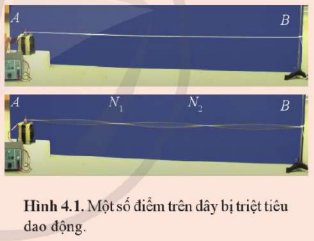
- Các điểm dao động với biên độ cực đại là bụng sóng.
- Các điểm không dao động (đứng yên) là nút sóng.

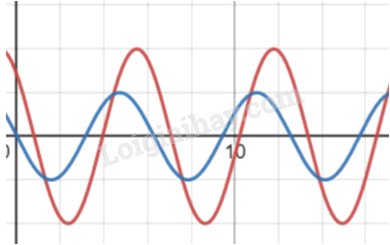
Hai dao động có cùng biên độ.
Ở cùng một thời điểm khi dao động 1 ở vị trí cân bằng thì dao động 2 ở vị trí bên và ngược lại.

Dao động 1 vẽ với biên độ A và chu kì T
Dao động 2 có cùng chu kì với dao động 1 và biên độ \(A_2=2A\) vị trí đầu tiên của dao động thứ hai bằng \(\dfrac{\sqrt{2}}{2}A_2\) và ở thời điểm \(\dfrac{T}{8}\) thì dao động 2 sẽ đi qua vị trí cân bằng.
Cứ thế tiếp tục vẽ 2 chu kì dao động của hai dao động
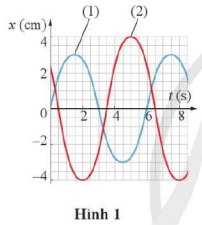
Đường màu xanh là dao động thứ nhất, đường màu đỏ là dao động thứ 2

a) Vì hai điểm gần nhất trên cùng phương truyền sóng dao động lệch pha nhau một góc \(\dfrac{\pi}{2}\)
Khoảng cách giữa hai điểm là 360cm= \(\dfrac{3\lambda}{2}\) nên hai điểm này dao động ngược pha nhau độ lệch pha của chúng là π
b) Sau 0,1s sóng truyền được khoảng cách là 0,1.330 = 33m = \(\dfrac{55\lambda}{4}\)
Độ lệch pha là \(\dfrac{3\pi}{4}\)

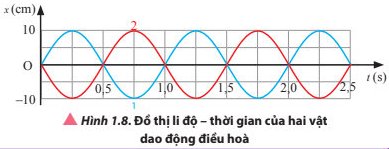
a) Dao động 1 (đường màu xanh) có:
- Biên độ: A1 = 3 cm
- Chu kì: T = 6 s
- Tần số: \(f=\dfrac{1}{T}=\dfrac{1}{6}\left(Hz\right)\)
Dao động 2 (đường màu đỏ) có:
- Biên độ: A2 = 4 cm
- Chu kì: T = 6 s
- Tần số: \(f=\dfrac{1}{T}=\dfrac{1}{6}\left(Hz\right)\)
b) Hai dao động có cùng chu kì nên \(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{6}=\dfrac{\pi}{3}\left(rad/s\right)\)
Độ lệch thời gian của hai dao động khi cùng trạng thái: \(\Delta t=2,5s\)
Độ lệch pha: \(\Delta\varphi=\omega.\Delta t=\dfrac{\pi}{3}\cdot2,5=150^o\)
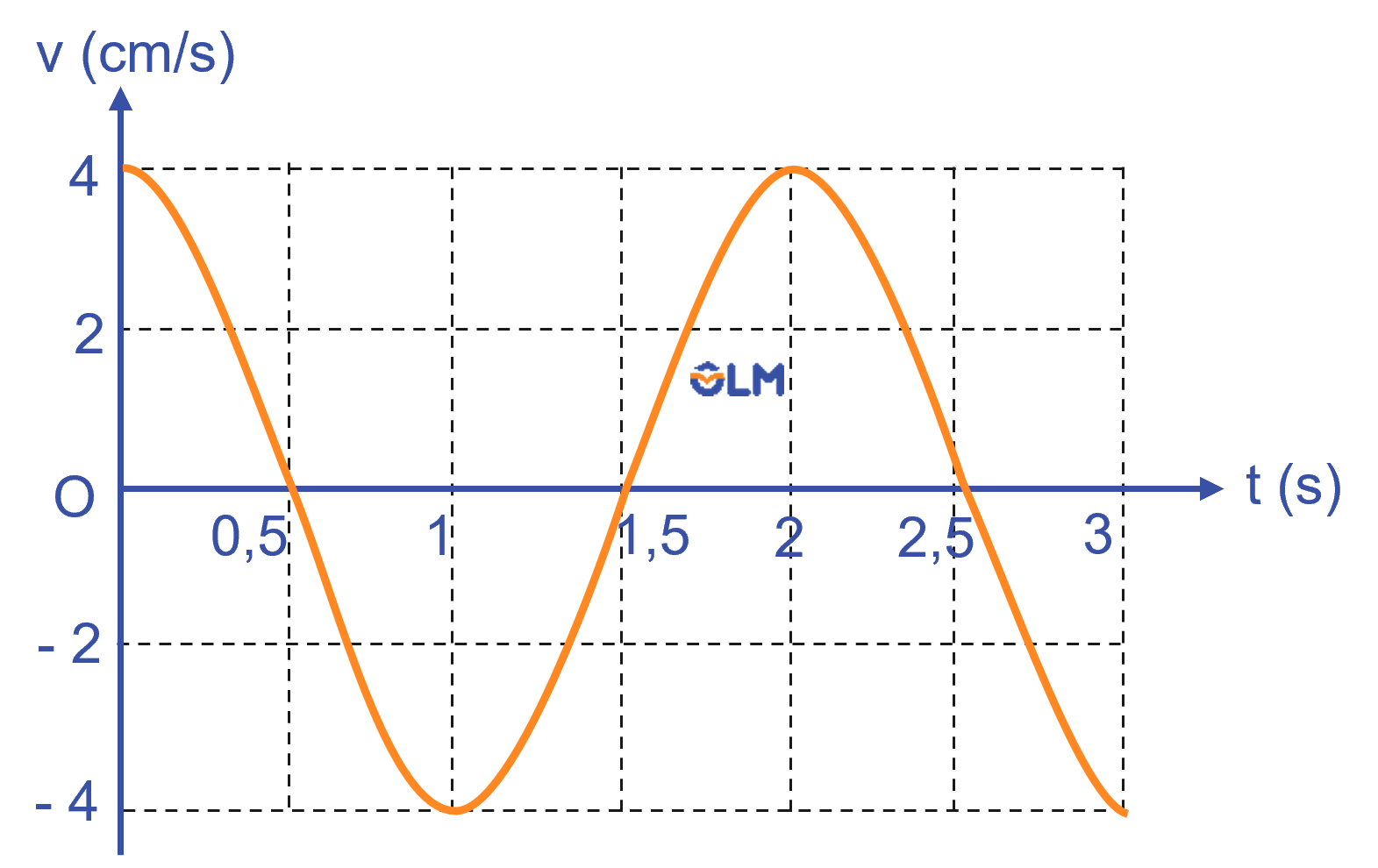
c) Tại thời điểm 3,5 s vật 2 đang ở VTCB nên vận tốc cực đại:
\(v=\omega A_2=\text{ }\dfrac{\pi}{3}\cdot4=\dfrac{4\pi}{3}\left(cm/s\right)\)
d) Tại thời điểm 1,5 s vật 1 đang ở biên dương nên gia tốc có giá trị:
\(a=-\omega^2A_1=-\dfrac{\pi^2}{9}\cdot3=-\dfrac{\pi^2}{3}\left(cm/s^2\right)\)
Độ lớn gia tốc khi đó là \(\dfrac{\pi^2}{3}cm/s^2\)
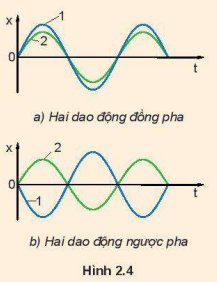


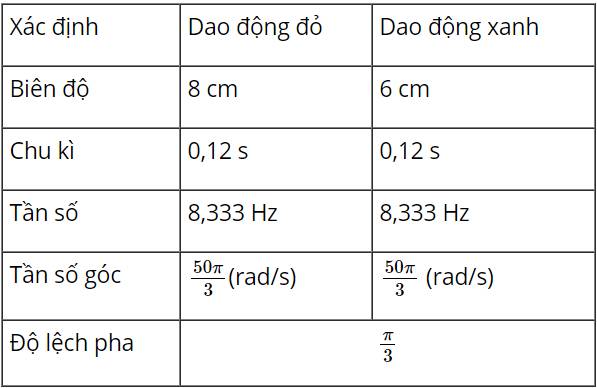
Độ lệch pha của hai dao động ở thời điểm t bất kì là: \(\Delta\phi=\left(\omega_2t+\varphi_2\right)-\left(\omega_1t+\varphi_1\right)\)
Vì 2 dao động có cùng chu kì nên \(\omega_1=\omega_2\)
Vậy \(\Delta\phi=\varphi_2-\varphi_1\)