Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét \(I=\int\limits^1_0x^2f\left(x\right)dx\)
Đặt \(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=x^2dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=\dfrac{1}{3}x^3\end{matrix}\right.\)
\(\Rightarrow I=\dfrac{1}{3}x^3.f\left(x\right)|^1_0-\dfrac{1}{3}\int\limits^1_0x^3.f'\left(x\right)dx=-\dfrac{1}{3}\int\limits^1_0x^3f'\left(x\right)dx\)
\(\Rightarrow\int\limits^1_0x^3f'\left(x\right)dx=-1\)
Lại có: \(\int\limits^1_0x^6.dx=\dfrac{1}{7}\)
\(\Rightarrow\int\limits^1_0\left[f'\left(x\right)\right]^2dx+14\int\limits^1_0x^3.f'\left(x\right)dx+49.\int\limits^1_0x^6dx=0\)
\(\Rightarrow\int\limits^1_0\left[f'\left(x\right)+7x^3\right]^2dx=0\)
\(\Rightarrow f'\left(x\right)+7x^3=0\)
\(\Rightarrow f'\left(x\right)=-7x^3\)
\(\Rightarrow f\left(x\right)=\int-7x^3dx=-\dfrac{7}{4}x^4+C\)
\(f\left(1\right)=0\Rightarrow C=\dfrac{7}{4}\)
\(\Rightarrow I=\int\limits^1_0\left(-\dfrac{7}{4}x^4+\dfrac{7}{4}\right)dx=...\)

a)
Ta có:
∫π20cos2xsin2xdx=12∫π20cos2x(1−cos2x)dx=12∫π20[cos2x−1+cos4x2]dx=14∫π20(2cos2x−cos4x−1)dx=14[sin2x−sin4x4−x]π20=−14.π2=−π8∫0π2cos2xsin2xdx=12∫0π2cos2x(1−cos2x)dx=12∫0π2[cos2x−1+cos4x2]dx=14∫0π2(2cos2x−cos4x−1)dx=14[sin2x−sin4x4−x]0π2=−14.π2=−π8
b)
Ta có: Xét 2x – 2-x ≥ 0 ⇔ x ≥ 0.
Ta tách thành tổng của hai tích phân:
∫1−1|2x−2−x|dx=−∫0−1(2x−2−x)dx+∫10(2x−2−x)dx=−(2xln2+2−xln2)∣∣0−1+(2xln2+2−xln2)∣∣10=1ln2∫−11|2x−2−x|dx=−∫−10(2x−2−x)dx+∫01(2x−2−x)dx=−(2xln2+2−xln2)|−10+(2xln2+2−xln2)|01=1ln2
c)
∫21(x+1)(x+2)(x+3)x2dx=∫21x3+6x2+11x+6x2dx=∫21(x+6+11x+6x2)dx=[x22+6x+11ln|x|−6x]∣∣21=(2+12+11ln2−3)−(12+6−6)=212+11ln2∫12(x+1)(x+2)(x+3)x2dx=∫12x3+6x2+11x+6x2dx=∫12(x+6+11x+6x2)dx=[x22+6x+11ln|x|−6x]|12=(2+12+11ln2−3)−(12+6−6)=212+11ln2
d)
∫201x2−2x−3dx=∫201(x+1)(x−3)dx=14∫20(1x−3−1x+1)dx=14[ln|x−3|−ln|x+1|]∣∣20=14[1−ln2−ln3]=14(1−ln6)∫021x2−2x−3dx=∫021(x+1)(x−3)dx=14∫02(1x−3−1x+1)dx=14[ln|x−3|−ln|x+1|]|02=14[1−ln2−ln3]=14(1−ln6)
e)
∫π20(sinx+cosx)2dx=∫π20(1+sin2x)dx=[x−cos2x2]∣∣π20=π2+1∫0π2(sinx+cosx)2dx=∫0π2(1+sin2x)dx=[x−cos2x2]|0π2=π2+1
g)
I=∫π0(x+sinx)2dx∫π0(x2+2xsinx+sin2x)dx=[x33]∣∣π0+2∫π0xsinxdx+12∫π0(1−cos2x)dxI=∫0π(x+sinx)2dx∫0π(x2+2xsinx+sin2x)dx=[x33]|0π+2∫0πxsinxdx+12∫0π(1−cos2x)dx
Tính :J=∫π0xsinxdxJ=∫0πxsinxdx
Đặt u = x ⇒ u’ = 1 và v’ = sinx ⇒ v = -cos x
Suy ra:
J=[−xcosx]∣∣π0+∫π0cosxdx=π+[sinx]∣∣π0=πJ=[−xcosx]|0π+∫0πcosxdx=π+[sinx]|0π=π
Do đó:
I=π33+2π+12[x−sin2x2]∣∣π30=π33+2π+π2=2π3+15π6

Tham khảo:
Giả sử hàm số f(x) là hàm số chẵn trên đoạn [-a; a], ta có:
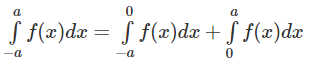
Đổi biến x = - t đối với tích phân
Ta được:
Vậy
Trường hợp sau chứng minh tương tự. Áp dụng:
Vì
là hàm số lẻ trên đoạn [-2; 2] nên

a) =
=
b) =
=
=
c)=
d)=
=
e)=
=
g)Ta có f(x) = sin3xcos5x là hàm số lẻ.
Vì f(-x) = sin(-3x)cos(-5x) = -sin3xcos5x = f(-x) nên:

Câu 1:
\(\int\limits^3_0\left(f'\left(x\right)+1\right)\sqrt{x+1}dx=\int\limits^3_0f'\left(x\right)\sqrt{x+1}dx+\int\limits^3_0\sqrt{x+1}dx\)
\(=\int\limits^3_0f'\left(x\right)\sqrt{x+1}dx+\frac{14}{3}=\frac{302}{15}\Rightarrow\int\limits^1_0f'\left(x\right)\sqrt{x+1}dx=\frac{232}{15}\)
Ta có:
\(I=\int\limits^3_0\frac{f\left(x\right)dx}{\sqrt{x+1}}\)
Đặt \(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=\frac{dx}{\sqrt{x+1}}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=2\sqrt{x+1}\end{matrix}\right.\)
\(\Rightarrow I=2f\left(x\right)\sqrt{x+1}|^3_0-2\int\limits^3_0f'\left(x\right)\sqrt{x+1}dx\)
\(=4f\left(3\right)-2f\left(0\right)-2.\frac{232}{15}\)
\(=2\left(2f\left(3\right)-f\left(0\right)\right)-\frac{464}{15}=36-\frac{464}{15}=\frac{76}{15}\)
Câu 2:
\(I_1=\int\limits^3_1\frac{xf'\left(x\right)}{x+1}dx=0\)
Đặt \(\left\{{}\begin{matrix}u=\frac{x}{x+1}\\dv=f'\left(x\right)dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\frac{1}{\left(x+1\right)^2}dx\\v=f\left(x\right)\end{matrix}\right.\)
\(\Rightarrow I_1=\frac{xf\left(x\right)}{x+1}|^3_1-\int\limits^3_1\frac{f\left(x\right)}{\left(x+1\right)^2}=\frac{3.3}{3+1}-\frac{1.3}{1+1}-\int\limits^3_1\frac{f\left(x\right)}{\left(x+1\right)^2}dx=\frac{3}{4}-\int\limits^3_1\frac{f\left(x\right)}{\left(x+1\right)^2}dx=0\)
\(\Rightarrow\int\limits^3_1\frac{f\left(x\right)}{\left(x+1\right)^2}dx=\frac{3}{4}\)
Ta có:
\(I=\int\limits^3_1\frac{f\left(x\right)+lnx}{\left(x+1\right)^2}dx=\int\limits^3_1\frac{f\left(x\right)}{\left(x+1\right)^2}dx+\int\limits^3_1\frac{lnx}{\left(x+1\right)^2}dx=\frac{3}{4}+I_2\)
Xét \(I_2=\int\limits^3_1\frac{lnx}{\left(x+1\right)^2}dx\Rightarrow\) đặt \(\left\{{}\begin{matrix}u=lnx\\dv=\frac{1}{\left(x+1\right)^2}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\frac{dx}{x}\\v=\frac{-1}{x+1}\end{matrix}\right.\)
\(\Rightarrow I_2=\frac{-lnx}{x+1}|^3_1+\int\limits^3_1\frac{dx}{x\left(x+1\right)}=-\frac{1}{4}ln3+\int\limits^1_0\left(\frac{1}{x}-\frac{1}{x+1}\right)dx\)
\(=-\frac{1}{4}ln3+ln\left(\frac{x}{x+1}\right)|^3_1=-\frac{1}{4}ln3+ln\frac{3}{4}-ln\frac{1}{2}=\frac{3}{4}ln3-ln2\)
\(\Rightarrow I=\frac{3}{4}+\frac{3}{4}ln3-ln2\)
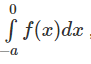
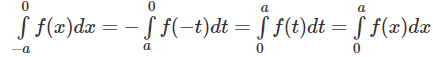
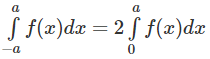

Lời giải:
\(\int ^{1}_{0}x^2dx=\left.\begin{matrix} 1\\ 0\end{matrix}\right|\frac{x^3}{3}=\frac{1}{3}; \int ^{1}_{0}x^3dx=\left.\begin{matrix} 1\\ 0\end{matrix}\right|\frac{x^4}{4}=\frac{1}{4}\)
\(\frac{1}{3}>\frac{1}{4}\Rightarrow A\) đúng.
Câu B. Xét về mặt điều kiện thì với \(x>0\Rightarrow \frac{1}{x+1}\) luôn có nghĩa, lúc này hàm số mới có tích phân được.
Xét theo định nghĩa nguyên hàm thì luôn đúng vì \(F(x)=\int f(x)dx\Leftrightarrow f(x)=F'(x)\)
Câu D.
\(\int ^b_af(x)dx+\int ^c_bf(x)dx=F(b)-F(a)+F(c)-F(b)\)
\(=F(c)-F(a)=\int ^c_af(x)dx\)
Do đó D đúng.
Do đó câu C sai.
Nếu \(\int ^a_{-a}f(x)dx=2\int ^{a}_0f(x)dx\)
\(\Leftrightarrow F(a)-F(-a)=2F(a)-2F(0)\)
\(\Leftrightarrow F(a)+F(-a)=2F(0)\)
Giả sử cho \(F(x)=x^2\), \(a\neq 0\)thì điều trên hiển nhiên vô lý
Do đó C sai.