Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có tam giác ABC cân tại A
=> góc B= góc C
=> 1/2 góc C= 1/2 góc B
=> ABE=ACF
Xét tam giác ABE và tam giác AFC có:
AB=AC(gt)
A(chung)
ABE=ACF(cmt)
=> tam giac ABE= tam giác ACF(g.c.g)
=> AF=AE
=> tam giác AEF cân tại A
b)Ta có góc B= góc C
=> 1/2 góc B=1/2 góc C=>EBC=FCB
Theo câu a, ta có tam giác ABE= tam giác ACF(g.c.g)
=> BE=CF
Xét tam giác BFC vá tam giác CEB có
BE=CF(tam giác ABE= tam giác ACF)
FCB=ECB(cmt)
BC(chung)
=> tam giác BFC= tam giác CEB(c.g.c0
c) Tam giác AFE cân tại A
=>góc AFE=(180*-A)/2
Tam giác ABC cân tại B=>ABC=(180*-A)/2
=> ABC=AFE
=> FE//BC(1)
Ta có: FB=AB-AF
EC=AC-AE
AB=AC
AF=AE
=> FB=EC(2)
Từ (1)(2)=> tứ giác BFEC là hình thang cân

a) ΔABC cân tại A suy ra
Ta lại có :
- ΔABM và ΔACN có
AB = AC (Do ΔABC cân tại A).
BM = CN(gt)
⇒ ΔABM = ΔACN (c.g.c)
⇒ AM = AN (hai góc tương ứng) ⇒ ΔAMN cân tại A.
b) Hai tam giác vuông BHM và CKN có
BM = CN (gt)
⇒ ΔBHM = ΔCKN (cạnh huyền – góc nhọn)
⇒ BH = CK (hai cạnh tương ứng)
c) Theo câu b ta có ΔBHM = ΔCKN ⇒HM = KN (hai góc tương ứng)
Mà AM = AN ⇒ AM –MH = AK – KN hay AH = AK.
d) ΔBHM = ΔCKN
Vậy tam giác OBC là tam giác cân tại O.
e) Khi góc BAC = 60º và BM = CN = BC
Tam giác cân ABC có góc BAC = 60º nên là tam giác đều
⇒ AB = BC và góc B1 = 60º
Ta có: AB = CB, BC = BM (gt) ⇒ AB = BM ⇒ ΔABM cân ở B ⇒
Mà theo tính chất góc ngoài trong ΔBAM thì
Tương tự ta có
Tam giác cân OBC có góc B3=60º nên ΔOBC là tam giác đều.
a) tam giác ABC cân
=> góc ABC=góc ACB
góc MBA+góc ABC=180độ (kề bù)
góc NCA+góc ACB=180độ(kề bù)
=> góc ABM=góc ACN
xét 2 tam giác ABM và ACN có:
AB=AC(tam giác ABC cân )
góc ABM=góc ACN(chứng minh trên)
BM=CN(gt)
=> 2 tam giác ABM=ACN(c.g.c)
=> AM=AN(2 cạnh tương ứng)
=> tam giác AMN cân ở A
b) tam giác AMN cân ở A
=> góc M=góc N
xét 2 tam giác MHB và NKC có:
góc MHB=góc NKC(=90độ)
MB=NC(gt)
góc M =góc N(chứng minh trên)
=> 2 tam giác MHB=NKC(cạnh huyền - góc nhọn)
=> BH=CK(2 cạnh tương ứng)
c) ta có : AM=AN (theo a)
HM=KN (tam giác MHB=tam giác NKC)
AM = AH+HM
AN= AK+ KN
=> AH= AK
d) tam giác MHB=tam giác NKC(theo b)
=> góc HBM=góc KCN(2 góc tương ứng)
góc HBM=góc OBC(đối đỉnh)
góc KCN=góc OCB(đối đỉnh)
=> góc OBC=góc OCB
=> tam giác OBC cân ở O
e) tam giác ABC có AB=AC ; góc BAC=60độ
=> tam giác ABC đều
=> AB=AC=BC
mà BC=BM(gt)
=> BM=AB
=>tam giác ABM cân ở B
góc ABC + góc ABM=180độ (kề bù)
=> góc ABM =180độ - góc ABC
=180độ-60độ
=120độ
tam giác ABC cân ở B
=> góc BAM=góc BMA =(180độ-góc ABM) / 2=1800−12002=6002=3001800−12002=6002=300
vậy góc AMN=30độ

Bài 2:
a: Xét ΔABE và ΔACF có
góc ABE=góc ACF
AB=AC
góc A chung
Do đó: ΔABE=ΔACF
Suy ra: AE=AF
b: Xét ΔABC có AF/AB=AE/AC
nên FE//BC
=>BFEC là hình thang
mà CF=BE
nên BFEC là hình thang cân
c: Xét ΔFEB có góc FEB=góc FBE
nên ΔFEB cân tại F
=>FE=FB=EC

a/vì AB//DC(gt) suy ra AB//DE
và AC//BE(gt)
do hai đoạn thẳng song song(AB//DE) chắn bởi 2 đường thẳng song song (AC//BE) suy ra AC=BE
Mà AC=BD(gt)
suy ra BD=BE
Trong tam giác BDE có BD=BE suy ra tam giác BDE cân tại B (dpcm)
b/Chứng minh:tg ACD=tg BDC
VÌ tg BDE cân tại B nên ta có :GÓc B1 = GÓc E1(*)
Vì AC//BE(gt)
E=C1 là 2 góc đồng vị
suy ra góc C1 =góc E(**)
từ (*);(**) suy ra B1=C1
bạn tự xét tg nha
suy ra tg ACD=tg BDC
c/bạn tự cm lun nha
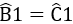
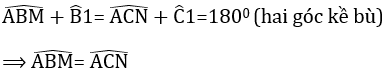
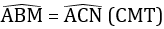
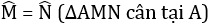

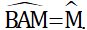
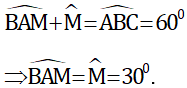
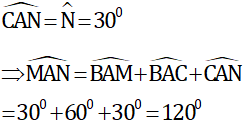
-ĐN:Tam giác cân là tam giác có 2 cạnh bằng nhau
- TC: Tam giác cân có 2 góc ở đáy bằng nhau
- PP chứng minh: + Chứng tam giác có 2 góc ở đáy bằng nhau
+ Chứng tam giác có 2 cạnh bằng nhau