Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tứ giác ADHE:
\(\widehat{AEH}+\widehat{ADH}=90^o+90^o=180^o.\)
Mà 2 góc này ở vị trí đối nhau.
\(\Rightarrow\) Tứ giác ADHE nội tiếp (dhnb).
b) Xét tứ giác BEDC:
\(\widehat{BEC}=\widehat{BDC}\left(=90^o\right).\)
Mà 2 đỉnh E; D kề nhau, cùng nhìn cạnh BC.
\(\Rightarrow\) Tứ giác BEDC nội tiếp (dhnb).
c) Sửa đề: Góc ACD \(\rightarrow\) Góc ACB.
Tứ giác BEDC nội tiếp (cmt).
\(\Rightarrow\widehat{AED}=\widehat{ACD}.\)
d) Tứ giác BEDC nội tiếp (cmt).
\(\Rightarrow\widehat{EDB}=\widehat{ECB}.\)

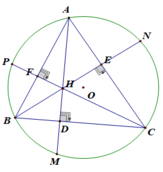
Cho tam giác nhọn ABC nội tiếp trong (O;R) có BD và CE là các đường cao. Cho góc A = 60 độ, tính theo R diện tích tứ giác OEAD
Có thể giải như sau:
Tam giác vuông ABD có ^BAD = 60o => AD = AB/2
Dễ thấy tg vuông ABD đồng dạng với tg vuông ACE => AD/AE = AB/AC => AD/AB = AE/AC => tg AED đông dạng tam giác ABC ( vì có chung góc A) => ED/BC = ADAB = 1/2 => ED = BC/2
Dễ tính được BC = RV3 => ED = RV3/2
Mặt khác : Vẽ đường kính AF => BF//CE (vì cùng _I_ với AB). Dễ thấy BCDE nội tiếp => ^BDE = ^BCE (cùng chắn cung BE) = ^CBF ( so le trong) = ^CAF (cùng chắn cung CF của (O) ) => AF _I_ DE ( vì đã có AD _I_ BD)
Vậy S(OEAD) = AO.ED/2 = R^2V3/4 => R = V(4SV3/3)
p/s:tham khảo

a) Xét tứ giác CEHD có:
∠(CED) = 90 0 (do BE là đường cao)
∠(HDC) = 90 0 (do AD là đường cao)
⇒ ∠(CED) + ∠(HDC) = 180 0
Mà ∠(CED) và ∠(HDC) là 2 góc đối của tứ giác CEHD nên CEHD là tứ giác nội tiếp

a, xét tứ giác BCDE có:
góc BEC = 90 độ
góc BDC = 90 độ
=>góc BEC=BDC
=>tứ giác BCDE nt
xét tứ giác ADHE có:
góc AEH = 90 độ
góc ADH=90 độ
=>AEH+ADH=180
=>tứ giác ADHE nt
b, vì tứ giác EDCB nt(cmt)
=>góc AED=ACB
xet tam giác AED và ACB có:
góc EAD chung
góc AED=ACB
=>2 tam giác này đồng dạng vs nhau
=>AE/AC=AD/AB
=>AD.AC=AE.AB
C, ta có :góc xAB=ACB
mak góc góc ACB=AED(cmt)
=>góc xAB=AED
=>Ax//ED

A B C E D H M K H
a) Xét tứ giác ADHE có:
\(\widehat{AEH}+\widehat{ADH}=90^o+90^o=180^o\)
=> tứ giác ADHE nội tiếp đường tròn đường kính AH.
b) hơi khó, mình chịu thôi, nhưng chỉ cần CM góc HED = góc EAM là mình sẽ làm được.

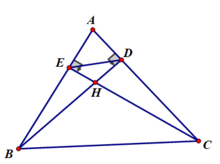
b) Xét tứ giác BDEC có:
∠(BEC) = ∠(BDC) = 90 0
Mà 2 góc này cùng nhìn cạnh BC
⇒ Tứ giác BDEC là tứ giác nội tiếp
a) Xét tứ giác AEHD có:
∠(AEH) = 90 0
∠(ADH) = 90 0
⇒∠(AEH) + ∠(ADH) = 180 0
⇒ Tứ giác AEHD là tứ giác nội tiếp.