Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

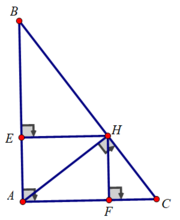
a) Xét tam giác ABC vuông tại A có:
A
B
2
+
A
C
2
=
B
C
2
⇒ 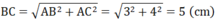
Ta có:
AH.BC = AB.AC ⇒ 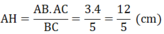
sinB = AC/BC = 4/5 ⇒ ∠B = 53 , 1 0
⇒ ∠C = 90 0 - ∠B = 36 , 9 0

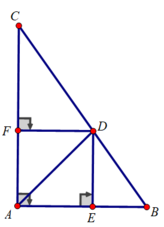
a) Xét tam giác ABC vuông tại A có:
B C 2 = A B 2 + A C 2 = 6 2 + 8 2 = 100
⇒ BC = 10 (cm)

∠B + ∠C = 90 0 ⇒ ∠C = 90 0 - 53 , 1 0 = 36 , 9 0

b)Để SMBC = SABC thì M phải cách BC một khoảng bằng AH. Do đó M phải nằm bên trên hai đường thẳng song song với BC, cách BC một khoảng bằng 3,6cm.

Giải
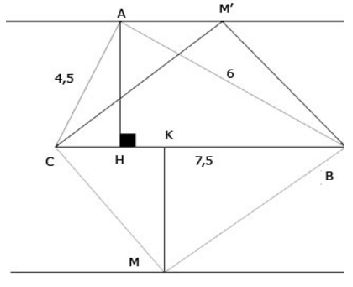
a. Xét \(\Delta ABC\) ta có :
\(AB^2+AC^2=\) \(6^2+4,5^2=56,25\) (cm)
\(BC^2=7,5^2=56,25\) (cm)
\(\Rightarrow\) \(\Delta ABC\) là tam giác vuông
b. - Áp dụng hệ thức về một số cạnh và đường cao trong tam giác vuông ta có :
AB.AC = BC.AH
\(\Leftrightarrow6.4,5=7,5.AH\)
\(\Leftrightarrow AH=\dfrac{6.4,5}{7,5}\)
\(\Leftrightarrow AH=3.6\) (cm)
- Trong \(\Delta ABH\perp H\) ta có :
sin B = \(\dfrac{AH}{AB}=\dfrac{3,6}{6}=0,6\)
\(\Rightarrow\) Góc B \(\approx\) \(37\) độ
\(\Rightarrow\) Góc C = 53 độ
Vậy AH = 3,6cm, góc B = 37 độ, góc C = 53 độ

a) Ta có AB^2+AC^2=6^2+8^2=100=10^2=BC^2
Vậy tam giác ABC vuông b)theo mình thì chứng minh da=de mới đúng
Xét tam giác BAD và tam giác BED có ^BAD=^BED(=90 độ)
Cạnh BD chung ^ABD=^DBE( hai tia phân giác )
Vậy tam giác BAD =tam giác BED =>AD=ED
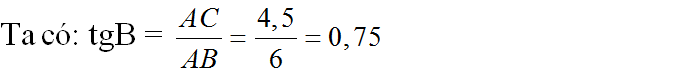
a) Xét tam giác ABC có:
A B 2 + A C 2 = 6 2 + 8 2 = 100 = B C 2
Tam giác ABC vuông tại A.