Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(n\left(\Omega\right)=C^2_5\)
\(n\left(A\right)=3\cdot2=6\)
=>P(A)=6/10=3/5
b: Giả sử không có sách toán
=>Chỉ có sách văn
=>\(n\left(\overline{B}\right)=2\)
=>\(P\left(\overline{B}\right)=\dfrac{2}{10}=\dfrac{1}{5}\)
=>P(B)=4/5

gọi số sách của Hòa là x ((sách) (x nguyên, x>0)
ta có:
x-10=3/2(100-x+10)
bấm máy ta đc x=70
suy ra hòa có 70 quyển, bình có 30 quyển
Giải theo lớp 5 dễ hơn nhé :
Nếu Hòa cho Bình 10 quyển sách thì tông số quyển của Hòa và Bình vẫn là 100 quyển
Tổng số phần bằng nhau là :
3 + 2 = 5 (phần)
Số quyển của Hòa lúc sau là :
100 : 5 x 3 = 60 (quyển)
Số quyển sách của Hòa lúc đầu là :
60 + 10 = 70 (quyển)
Số quyển sách của Bình lúc đầu là :
100 - 70 = 30 (quyển)

Gọi x là số quyển sách xưởng in được trong mỗi ngày theo kế hoạch ( x nguyên dương )
Số ngày in theo kế hoạch : 6000/x ( ngày )
Số quyển sách xưởng in được thực tế trong mỗi ngày : x + 300 ( quyển sách )
Số ngày in thực tế : 6000/[x+3]( ngày )
Theo đề bài ta có phương trình : 6000/x -6000/[x+3]= 1
<=> x^2 +300.x 1 800 000 = 0
Giải được : x1 = 1200 [nhận] ; x2 = -1500 [loại]
Vậy số quyển sách xưởng in được mỗi ngày theo kế hoạch là 1200 quyển sách
Gọi x là số quyển sách xưởng in được trong mỗi ngày theo kế hoạch ( x nguyên dương )
Số ngày in theo kế hoạch : 6000/x ( ngày )
Số quyển sách xưởng in được thực tế trong mỗi ngày : x + 300 ( quyển sách )
Số ngày in thực tế : 6000/[x+3]( ngày )
Theo đề bài ta có phương trình : 6000/x -6000/[x+3]= 1
<=> x^2 +300.x 1 800 000 = 0
Giải được : x1 = 1200 [nhận] ; x2 = -1500 [loại]
Vậy số quyển sách xưởng in được mỗi ngày theo kế hoạch là 1200 quyển sách

Gọi x là số sách in được trong 1 ngày theo kế hoạch
\(\Rightarrow\)Số sách in được mỗi ngày để hoàn thành sớm kế hoạch là x+300
\(\Rightarrow\)Thời gian in 6000 quyển sách theo kế hoạch là\(\frac{6000}{x}\)
\(\Rightarrow\)Thời gian in 6000 quyển sách để hoàn thành sớm kế hoạch là\(\frac{6000}{x+300}\)
Ta có phương trình \(\frac{6000}{x}\)=\(\frac{6000}{x+300}\)+1\(\Rightarrow\)x=1200(bạn tự giải phương trình nhé)
\(\Rightarrow\)Số quyển sách xương in được trong 1 ngày theo kế hoạch là 1200 quyển

bài này đơn giản mà:
Số sách ngăn trên ít hơn ngăn dưới:
35 + (15 – 10) x 2 = 45 (quyển)
Số sách ngăn trên lúc đầu là:
(135 – 45) : 2 = 45 (quyển)
Đ/S:.............

Gọi số sách Toán Hội khuyến học tỉnh tặng cho trường A là x quyển (0<x<245;x∈N)
Thì số sách Ngữ văn Hội khuyến học tỉnh tặng cho trường A là 245−x quyển
Số sách Toán nhà trường dùng để phát cho học sinh khó khăn là 12x quyển
Số sách Ngữ văn nhà trường dùng để phát cho học sinh khó khăn là 23(245−x) quyển
Vì mỗi bạn nhận được 1 quyển sách Toán và 1 quyển sách Ngữ văn nên số quyển sách Toán và quyển sách Ngữ Văn đem phát là bằng nhau.
Ta có phương trình 12x=23(245−x)
⇔12x=4903−2
⇔76x=4903
⇔x=4903:76
⇔x=140(tm)
Vậy số sách Toán Hội khuyến học tỉnh tặng cho trường A là 140 quyển.
Số sách Ngữ văn Hội khuyến học tỉnh tặng cho trường A là 245−140=105 quyển.
Gọi số sách ngữ văn và toán trường A được tặng lần lượt là x;yx;y (quyển) (0<x;y<245)(0<x;y<245) (x,y∈N)(x,y∈N)
Tổng số sách toán và ngữ văn là: y+x=245y+x=245 (quyển)
Số sách toán trường A phát cho các bạn học sinh có hoàn cảnh khó khăn là 12y12y
Số sách ngữ văn trường A phát cho học sinh có hoàn cảnh khó khăn là 23x23x
Mỗi bạn nhận được nhận 1 quyển toán và 1 quyển ngữ văn, nên số quyển toán phát cho các bạn phải bằng số quyển ngữ văn, ta có hệ phương trình:
⎧⎨⎩y+x=24512y=23x⇔⎧⎪ ⎪⎨⎪ ⎪⎩x+43x=245y=43x{y+x=24512y=23x⇔{x+43x=245y=43x
⇔{x=105y=140⇔{x=105y=140
Vậy số sách toán là 140 quyển, ngữ văn 105 quyển.

Gọi số bạn được tặng 3 quyển sách và số bạn được tặng 5 quyển sách lần lượt là x(bạn) và y(bạn)
(Điều kiện: \(x,y\in Z^+\))
Số bạn được tặng sách là 42 bạn nên x+y=42(1)
Số quyển sách tặng cho các bạn được tặng 3 quyển là:
3x(quyển)
Số quyển sách tặng cho các bạn được tặng 5 quyển là:
5y(quyển)
Tổng số quyển sách là 146 quyển nên 3x+5y=146(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}x+y=42\\3x+5y=146\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x+3y=126\\3x+5y=146\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2y=-20\\x+y=42\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=10\\x=42-x=42-10=32\end{matrix}\right.\left(nhận\right)\)
Vậy: Số bạn được tặng 3 quyển sách là 32 bạn
Số bạn được tặng 5 quyển sách là 10 bạn
Gọi số bạn tặng 3 quyển sách là x và số bạn tặng 5 quyển sách là y (x;y là các số nguyên dương)
Do lớp có 42 học sinh nên ta có: \(x+y=42\) (1)
Số sách đã tặng: \(3x+5y\)
Do cả lớp tặng được 146 quyển sách nên ta có: \(3x+5y=146\) (2)
Từ (1) và (2) ta có hệ: \(\left\{{}\begin{matrix}x+y=42\\3x+5y=146\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=32\\y=10\end{matrix}\right.\)

Gọi x (quyển sách) là số quyển sách xưởng in được trong mỗi ngày theo kế hoạch (x ∈ ℕ * )
Số ngày in theo kế hoạch: 6000/x (ngày)
Số quyển sách xưởng in được thực tế trong mỗi ngày: x + 300 (quyển sách)
Số ngày in thực tế: 6000/(x+300) (ngày)
Theo đề bài ta có phương trình:
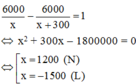
Vậy số quyển sách xưởng in được trong mỗi ngày theo kế hoạch là: 1200 (quyển sách)
Đáp án: D
a: Đặt quyển sách Ngữ Văn là A, quyển sách Mĩ Thuật là B, quyển sách Công Nghệ là C
=>\(\Omega=\left\{AB;BC;AC;BA;CB;CA\right\}\)
b: A: "Có 1 quyển sách Ngữ Văn được lấy ra"
=>A={AB;AC;BA;CA}
=>n(A)=4
=>\(P_A=\dfrac{4}{6}=\dfrac{2}{3}\)
B: "Cả hai quyển sách lấy ra đều là sách Mỹ Thuật"
=>\(B=\varnothing\)
=>P(B)=0