
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gửi Thắng Nguyễn: Mình không biết tại sao lại ko phân tích được?

\(\left(\frac{1}{2}xy-1\right).\left(x^3-2x-6\right)=\frac{1}{2}xy.\left(x^3-2x-6\right)+\left(-1\right).\left(x^3-2x-6\right)\)
= \(\frac{1}{2}xy.x^3+\frac{1}{2}xy.\left(-2x\right)+\frac{1}{2xy}.\left(-6\right)+\left(-1\right).x^3+\left(-1\right).\left(-2x\right)+\left(-1\right).\left(-6\right)\)
= \(\frac{1}{2}x^{\left(1+3\right)}y-x^{\left(1+1\right)}y-3xy-x^3+2x+6\)
= \(\frac{1}{2}x^4y-x^2y-3xy-x^3+2x+6\)
= \(\frac{1}{2}x^4y-x^3-x^2y-3xy+2x+6\)
Chúc bạn học tốt !!!
Bài làm
Ta có: ( xy - 1 )( x3 - 2x - 6 )
= ( xy . x3 ) + [ xy . ( -2x ) ] + [ xy . ( - 6 ) ] + [ ( -1 ) . x3 ] + [ ( -1 ) . ( -2x ) ] + [ ( -1 ) . ( -6 ) ] ( * chỗ này nếu thầnh thạo phép nnhân đa thức r thì k cần pk ghi đâu )
= x4y - 2x2y - 6xy - x3 + 2x + 6
# Học tốt #

\(x^4+2014x^2+2013x+2014\)
\(=x^4+2014x^2+2014x-x+2014\)
\(=\left(x^4-x\right)+\left(2014x^2+2014x+2014\right)\)
\(=x\left(x^3-1\right)+2014\left(x^2+x+1\right)\)
\(=x\left(x-1\right)\left(x^2+x+1\right)+2014\left(x^2+x+1\right)\)
\(=\left(x^2+x+1\right)\left(x^2-x+2014\right)\)
b)\(x^8+7x^4+6\)
\(=x^8+x^4+6x^4+6\)
\(=x^4\left(x^4+1\right)+6\left(x^4+1\right)\)
\(=\left(x^4+1\right)\left(x^4+6\right)\)
b) \(x^8+7x^4+16\)
\(=\left(x^8+8x^4+16\right)-x^4\)
\(=\left[\left(x^4\right)^2+2.x^4.4+4^2\right]-x^4\)
\(=\left(x^4+4\right)^2-\left(x^2\right)^2\)
\(=\left(x^4+4-x^2\right)\left(x^4+4+x^2\right)\)

Đặt
\(A=x^4-4x^3+8x+3\)
Giả sử
\(A=\left(x^2+ax+b\right)\left(x^2+cx+d\right)\)
\(=x^4+cx^3+dx^2+ax^3+acx^2+adx+bx^2+bcx+bd\)
\(=x^4+\left(a+c\right)x^3+\left(b+ac+d\right)x^2+\left(ad+bc\right)x+bd\)
\(\left[\begin{array}{nghiempt}a+c=-4\\b+ac+d=0\\ad+bc=8\\bd=3\end{array}\right.\)
\(\left[\begin{array}{nghiempt}a=-2\\b=-3\\c=-2\\d=-1\end{array}\right.\)
\(A=\left(x^2-2x-3\right)\left(x^2-2x-1\right)\)
dài dòng
\(x^4-4x^3+8x+3=x^4-2x^3-2x^3-x^2+4x^2-3x^2+2x+6x+3\)
\(=\left(x^4-2x^3-x^2\right)-\left(2x^3-4x^2-2x\right)-\left(3x^2-6x-3\right)\)
\(=x^2\left(x^2-2x-1\right)-2x\left(x^2-2x-1\right)-3\left(x^2-2x-1\right)\)
\(=\left(x^2-2x-1\right)\left(x^2-2x-3\right)\)

a) Đặt: x = a- b; y = b - c ; z = c- a
Ta có: x + y + z = 0
=> \(A=x^3+y^3+z^3=3xyz+\left(x+y+z\right)\left(x^2+y^2+z^2-xy-xz-yz\right)=3xyz\)
=> \(A=3xyz=3\left(a-b\right)\left(b-c\right)\left(c-a\right)\)
b) Đặt: \(a=x^2-2x\)
Ta có: \(B=a\left(a-1\right)-6=a^2-a-6=\left(a+2\right)\left(a-3\right)=\left(x^2-2x+2\right)\left(x^2-2x-3\right)\)
\(=\left(x^2-2x+2\right)\left(x+1\right)\left(x-3\right)\)
d) \(D=4\left(x^2+2x-8\right)\left(x^2+7x-8\right)+25x^2\)
Đặt: \(x^2-8=t\)
Ta có: \(D=4\left(t+2x\right)\left(t+7x\right)+25x^2\)
\(=4t^2+36xt+81x^2=\left(2t+9x\right)^2\)
\(=\left(2x^2+9x-16\right)^2\)

a) x(x-y) + y(x+y) = x^2 - xy + yx + y^2 = x^2 + y^2 = (-6)^2 + 8^2 = 100
b) x(x^2 - y ) - x^2( x + y ) + y(x^2 - x )
= x^3 - xy - x^3 -x^2y+yx^2 - xy
= ( x^3 - x^3 ) + ( x^2 y - x^2 y ) + ( -xy - xy )
= -2xy
Bạn kiểm tra lại đề nhé!


x^2 + 2y^2 - 2y - 2xy + 1 = (x^2 - 2xy + y^2) + (y^2 - 2y + 1) = (x - y)^2 + (y - 1)^2
\(x^2+2y^2-2y-2xy+1\)
\(=x^2-2xy+y^2+y^2-2y+1\)
\(=\left(x-y\right)^2+\left(y-1\right)^2\)
\(=\left(x-y\right)^2-\left(1-y\right)^2\)
\(=\left(x-y-1+y\right)\left(x-y+1-y\right)\)
\(=\left(x-1\right)\left(x-2y+1\right)\)
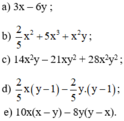
 xy – 1 với đa thức x3 – 2x – 6.
xy – 1 với đa thức x3 – 2x – 6.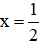 và y = –100;
và y = –100;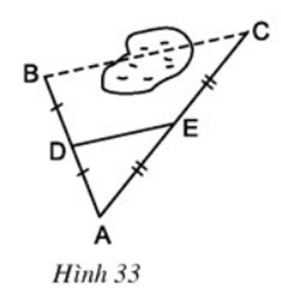
a) 3x – 6y
= 3.x – 3.2y
(Xuất hiện nhân tử chung là 3)
= 3(x – 2y)
c) 14x2y – 21xy2 + 28x2y2
= 7xy.2x – 7xy.3y + 7xy.4xy
(Xuất hiện nhân tử chung 7xy)
= 7xy(2x – 3y + 4xy)
e) 10x(x – y) – 8y(y – x)
(Nhận thấy x – y = –(y – x) nên ta đổi y – x về x – y)
= 10x(x – y) – 8y[–(x – y)]
= 10x(x – y) + 8y(x – y)
= 2(x – y).5x + 2(x – y).4y
(Xuất hiện nhân tử chung 2(x – y))
= 2(x – y)(5x + 4y)