Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ps đc viết dưới dạng số thập phân hữu hạn : \(\frac{1}{4};\frac{13}{50};-\frac{17}{125};\frac{7}{14}\)
ps đc viết dưới dạng só thập phân vô hạn tuần hoàn : \(-\frac{5}{6};\frac{11}{45}\)
\(\frac{1}{4}=0,25;\frac{13}{50}=0,26;-\frac{17}{125}=-0,136;\frac{7}{14}=0,5\)
\(-\frac{5}{6}=-0,8\left(3\right);\frac{11}{45}=0,2\left(4\right)\)

Vì mẫu của các phân số này không có ước nguyên tố khác 2 và 5.
\(\dfrac{-7}{16}=-0,4375\)
\(\dfrac{2}{125}=0,016\)
\(\dfrac{11}{40}=0,275\)
\(\dfrac{-14}{25}=-0,56\).
Các phân số \(\dfrac{-7}{16};\dfrac{2}{125};\dfrac{11}{40};\dfrac{-14}{25}\)viết được dưới dạng số thập phân hữu hạn vì mẫu số của các phân số đó chỉ có thừa số nguyên 2 và 5.
\(\dfrac{-7}{16}=-0,4357\)
\(\dfrac{2}{125}=0,016\)
\(\dfrac{11}{40}=0,275\)
\(\dfrac{-14}{25}=-0,56\)

- \(\frac{3}{8}\) đc viết dưới dạng số thập phân hữu hạn vì có mẫu là 8 = 23 (ko có ước nguyên tố khác 2 và 5)
- \(\frac{-7}{5}\) đc viết dưới dạng số thập phân hữu hạn vì có mẫu là 5 = 5 (ko có ước nguyên tố khác 2 và 5)
- \(\frac{13}{20}\) đc viết dưới dạng số thập phân hữu hạn vì có mẫu là 20 = 22.5 (ko có ước nguyên tố khác 2 và 5)
\(\frac{-13}{125}\) đc viết dưới dạng số thập phân hữu hạn vì có mẫu là 125 = 53 (ko có ước nguyên tố khác 2 và 5)
Tick cho mình với nha!!!!!!!!

1) Vì mẫu của chúng không chứa ước nguyên tố khác 2 và 5:
3/8 có mẫu 8 = 2^3
-7/5 có mẫu 5 = 5
13/20 có mẫu 20 = 2^2 . 5
-13/125 có mẫu 125 = 5^3
Nên: các phân số trên viết được dưới dạng số thập phân hữu hạn
Ta có: 3/8 = 0,375
-7/5 = -1,4
13/20 = 0,65
-13/125 = -0,104

1) Ta có:
\(-\dfrac{7}{16}\) = -0,4375 => Số thập phân hữu hạn.
\(\dfrac{2}{125}\) = 0,016 => Số thập phân hữu hạn.
\(-\dfrac{5}{3}\) = -1,66...=> Số thập phân vô hạn tuần hoàn.
\(\dfrac{12}{-24}\) = -0,5 => Số thập phân hữu hạn.
\(\dfrac{3}{12}\) = 0,25 => Số thập phân hữu hạn.
2)
a) 0,12 = \(\dfrac{12}{100}\) = \(\dfrac{3}{25}\)
b) 2,125 = \(\dfrac{2125}{1000}\) = \(\dfrac{17}{8}\)

Các phân số đã cho có mẫu dương và các mẫu đó lần lượt là 8 = , 5, 20 =
. 5, 125 =
đều không chứa thừa số nguyên tố nào khác 2 và 5 nên chúng được viết dưới dạng số thập phân hữu hạn
Ta được :
Các phân số đã cho có mẫu dương và các mẫu đó lần lượt là 8 = 2323, 5, 20 = 2222. 5, 125 = 5353 đều không chứa thừa số nguyên tố nào khác 2 và 5 nên chúng được viết dưới dạng số thập phân hữu hạn
Ta được;
38=0,375;−75=−1,4;1320=0,65;−13125==0,104
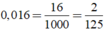
Ta có: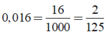
Chọn đáp án A.