Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có số hạng tổng quát của dãy số \({u_n} = 5n + 1\;\left( {n\; \in {N^*}} \right)\).
b) Các số hạng của dãy số là: 6; 11; 16; 21; 26.
Số hạng đầu của dãy số là: 6 và số hạng cuối của dãy số là 26.

a) Vì hàm số \(u\) xác định trên tập hợp các số nguyên dương
\(\mathbb{N}^{\text{∗
}}\) nên nó là một dãy số vô hạn.
b) Ta có:
\(u_1=1^3=1\\ u_2=2^3=8\\ u_3=3^3=27\\ u_4=4^3=64\\ u_5=5^3=125.\)

a) Gọi \(\left(S_n\right)\) là dãy số chỉ diện tích của \(5\) hình tròn với \(S_n=\pi n^2\).Ta có:
\(S_1=\pi.1^2=\pi\\ S_2=\pi.2^2=4\pi\\ S_3=\pi.3^2=9\pi\\ S_4=\pi.4^2=16\pi\\ S_5=\pi.5^2=25\pi.\)
Vậy dãy số chỉ diện tích của \(5\) hình tròn là:\(\pi;4\pi;9\pi;16\pi;25\pi.\)
b) Số hạng đầu:\(S_1=\pi\);số hạng cuối:\(S_5=25\pi.\)

a, Quy luật: Mỗi số hạng kể từ số thứ hai bằng số hạng đứng trước nó chia cho 2.
Vậy ba số hạng tiếp theo là: \(a_5=1;a_6=\dfrac{1}{2};a_7=\dfrac{1}{4}\)
b, Các số hạng của dãy số có dạng \(2^n\) với số mũ của số liền sau ít hơn số mũ của số liền trước 1 đơn vị.
Vậy ta có thể viết ba số hạng tiếp theo là: \(a_5=a^0;a_6=a^{-1};a_7=a^{-2}\)

Ta thấy quy luật của dãy này là dãy các số nguyên tố liên tiếp tăng dần. Do đó \(u_8\) chính là số nguyên tố thứ 8 hay \(u_8=19\).

a) Năm số hạng đầu của dãy số là: \(u_1=1^2=1;u_2=2^2=4;u_3=3^2=9;u_4=4^2=16;u_5=5^2=25\).
Số hạng tổng quát của dãy số un là \(u_n=n^2\) với n ∈ ℕ.
b) Dạng khai triển của dãy số \(u_1=1,u_2=4,u_3=9,u_4=16,...u_n=n^2\) ...

Ta có: \({u_n} - {u_{n - 1}} = \left( {4n - 3} \right) - \left[ {4\left( {n - 1} \right) - 3} \right] = 4,\;\forall n \ge 2\).
Vậy \(\left( {{u_n}} \right)\) là một cấp số cộng với số hạng đầu \({u_1} = 1\) và công sai \(d = 4\)
Số hạng tổng quát \({u_n} = 1 + 4\left( {n - 1} \right)\).

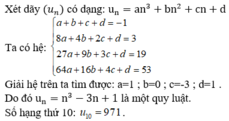
Số hạng đầu của khai triển là u1 = u(1) = 13 = 1.
Số hạng cuối của khai triển là u5 = u(5) = 53 = 125.
Dãy số được viết dưới dạng khai triển là: 1; 8; 27; 64; 125.