Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

22/Động lượng của hệ có độ lớn là :
\(\Delta p=\sqrt{p_1^2+p_2^2}=\sqrt{\left(3.4\right)^2+\left(2.8\right)^2}\)
\(=20kgm\text{/}s\)
Vậy ta chọn C
39/Theo bảo toàn động lượng ta có:
\(m_1v_1-m_2v_2=-m_1+0\)
\(50.2-80.v_2=-50.2\Rightarrow v_2=2,5m\text{/}s\)
Vậy ta chọn B

giải
động lượng của vật 1: \(\overrightarrow{P1}=m1.\overrightarrow{V1}\)
động lượng của vật 2: \(\overrightarrow{P2}=m2.\overrightarrow{V2}\)
động lượng của hệ:\(\overrightarrow{P}=\overrightarrow{P1}+\overrightarrow{P2}=m1.\overrightarrow{V1}+m2.\overrightarrow{V2}\)
vecto động lượng \(\overrightarrow{P}\) được xác định như hình vẽ (hình tự vẽ nhé)
áp dụng hệ thức lượng trong tam giác thường ta có
\(\sqrt{P1^2+P2^2+2P1P2.\cos90^O}=2,24kg.m/s\)
chiếu hệ thức vecto: \(\overrightarrow{P}=\overrightarrow{P1}+\overrightarrow{P2}\) xuống phương của \(\overrightarrow{P2}\) ta có
\(P.\cos a=P2+P1.\cos90^O\)
\(\Rightarrow\cos a=\frac{P2+P1.\cos90^o}{P}=\frac{2+1.0}{2,24}=0,898\Rightarrow a\approx55^o\)
vậy vecto động lượng \(\overrightarrow{P}\) có độ lớn 2,24kg.m/s và hợp lực với vận tốc \(\overrightarrow{V2}\) một góc \(55^o\)
Vì hướng vuông góc nên \(p=\sqrt{p_1^2+p_2^2}\)
\(\Leftrightarrow p=\sqrt{\left(1.1\right)^2+\left(1.2\right)^2}\)
\(\Leftrightarrow p=\sqrt{1+4}\)
\(\Leftrightarrow p=2,2\left(kg.m/s\right)\)
Vậy ...

Ta có:
p → = p → 1 + p → 2 v à p 1 = m 1 . v 1 = 2.4 = 8 ( k g . m / s ) ; p 2 = m 2 . v 2 = 3.2 = 6 ( k g . m / s )
a. Vì v → 2 cùng hướng với v 1 → ⇒ p → 1 , p → 2 cùng phương, cùng chiều
⇒ p = p 1 + p 2 = 8 + 6 = 14 ( k g . m / s )
![]()
b. Vì v → 2 ngược hướng với v 1 → ⇒ p → 1 , p → 2 cùng phương, ngược chiều
⇒ p = p 1 − p 2 = 8 − 6 = 2 ( k g . m / s )
![]()
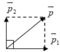
c. Vì v → 2 hướng chếch lên trên, hợp với v 1 → góc 900 ⇒ p → 1 , p → 2 vuông góc
⇒ p = p 1 2 + p 2 2 = 8 2 + 6 2 = 10 ( k g . m / s )
d. Vì v → 2 hướng chếch lên trên, hợp với góc 600 ⇒ p → 1 , p → 2 tạo với nhau một góc 60 o
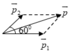
⇒ p 2 = p 1 2 + p 2 2 + 2 p 1 p 2 cos α ⇒ p = 8 2 + 6 2 + 2.8.6 cos 60 0 = 2 37 ( k g . m / s )

Bài tập 2: Một vật có m = 1kg đang chuyển động với vận tốc v = 2m/s. Tính động lượng của vật?
________________________________________________________________
Động lượng của vật: \(p=m.v=1.2=2\left(kg.m/s\right)\)
Vậy ..........
Bài tập 3: Một vật có khối lượng m = 2kg, có động lượng 6kg.m/s, vật đang chuyển động với vận tốc bao nhiêu?
Vận tốc vận đang chuyển động:
\(v=\frac{p}{m}=\frac{6}{2}=3m/s\)
Vậy............
Câu 3 :
Ta có : \(W_đ=\frac{1}{2}m.v^2\)
Vật chuyển động với vận tốc :
\(\Leftrightarrow v=\sqrt{\frac{W_đ}{\frac{1}{2}.m}=}\sqrt{\frac{6}{\frac{1}{2}.2}}=\) \(2,4\)m/s

Động lượng của vật I:
\(\overrightarrow{p_1}=m_1\overrightarrow{v_1}\)
Động lượng của vật II:
\(\overrightarrow{p_2}=m_2\overrightarrow{v_2}\)
Động lượng của hệ:
\(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}=m_1\overrightarrow{v_1}+m_2\overrightarrow{v_2}\)
Vecto động lượng \(\overrightarrow{p}\) được xác định như hình vẽ.
Áp dụng hệ thức lượng trong tam giác thường, ta có:
\(\sqrt{p^2_1++p^2_2+2p_1p_2.cos60^o}=2,65kg.m\text{/}s\)
Chiếu hệ thức vecto \(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}\) xuống phương của \(\overrightarrow{p_2}\) , ta có:
\(p.cos\alpha=p_2+p_1.cos60^o\)
\(\Rightarrow cos\alpha=\frac{p_2+p_1.cos60^o}{p}=\frac{2+1.0,5}{2,65}=0,943\Rightarrow\alpha=39^o\)
Vậy vecto động lượng \(\overrightarrow{p}\) có độ lớn \(2,65kg.m\text{/}s\) và hợp lực với vận tốc \(\overrightarrow{v_2}\)một góc\(39^o\)
Tham khảo